Matrix algebra for a data scientist
This article begins a series for anyone who finds matrix algebra overwhelming. My goal is to turn what you’re afraid of into what you’re fascinated by. You’ll find it especially helpful if you want to understand machine learning concepts and methods.
Table of contents:
- Introduction
- Prerequisites
- Matrix-vector multiplication
- Transposition
- Composition of transformations
- Inverse transformation
- Non-invertible transformations
- Determinant
- Non-square matrices
- Inverse and Transpose: similarities and differences
- Translation by a vector
- Final words
1. Introduction
You’ve probably noticed that while it’s easy to find materials explaining matrix computation algorithms, it’s harder to find ones that teach how to interpret complex matrix expressions. I’m addressing this gap with my series, focused on the part of matrix algebra that is most commonly used by data scientists.
We’ll focus more on concrete examples rather than general formulas. I’d rather sacrifice generality for the sake of clarity and readability. I’ll often appeal to your imagination and intuition, hoping my materials will inspire you to explore more formal resources on these topics. For precise definitions and general formulas, I’d recommend you look at some good textbooks: the classic one on linear algebra¹ and the other focused on machine learning².
This part will teach you
to see a matrix as a representation of the transformation applied to data.
Let’s get started then — let me take the lead through the world of matrices.
2. Prerequisites
I’m guessing you can handle the expressions that follow.
This is the dot product written using a row vector and a column vector:
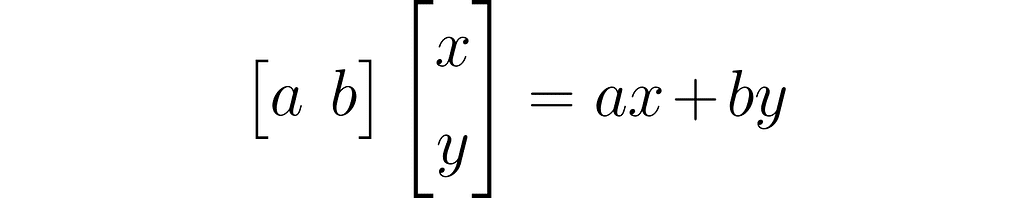
A matrix is a rectangular array of symbols arranged in rows and columns. Here is an example of a matrix with two rows and three columns:
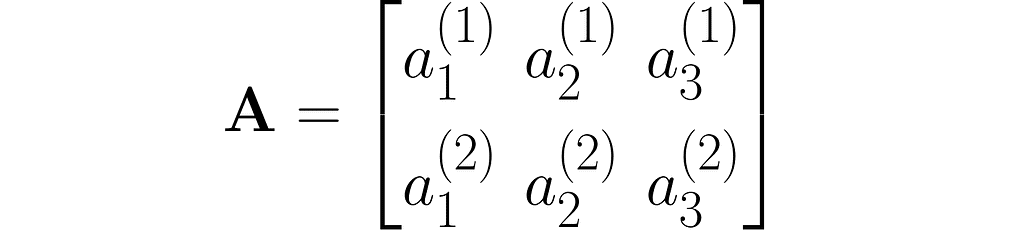
You can view it as a sequence of columns
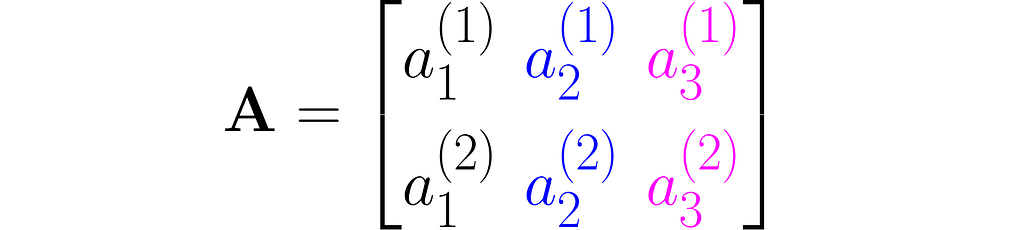
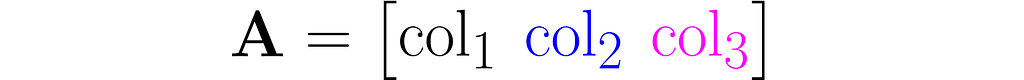
or a sequence of rows stacked one on top of another:
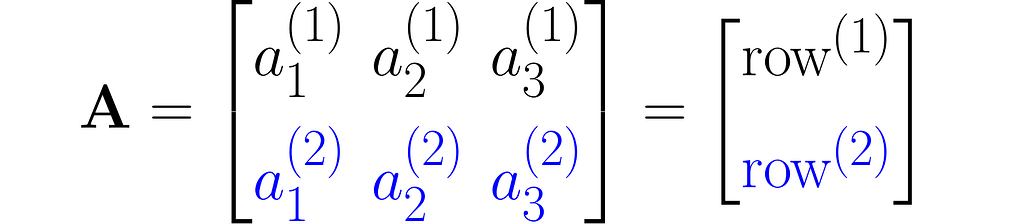
As you can see, I used superscripts for rows and subscripts for columns. In machine learning, it’s important to clearly distinguish between observations, represented as vectors, and features, which are arranged in rows.
Other interesting ways to represent this matrix are A₂ₓ₃ and A[aᵢ⁽ʲ ⁾].
Multiplying two matrices A and B results in a third matrix C = AB containing the scalar products of each row of A with each column of B, arranged accordingly. Below is an example for C₂ₓ₂ = A₂ₓ₃B₃ₓ₂.
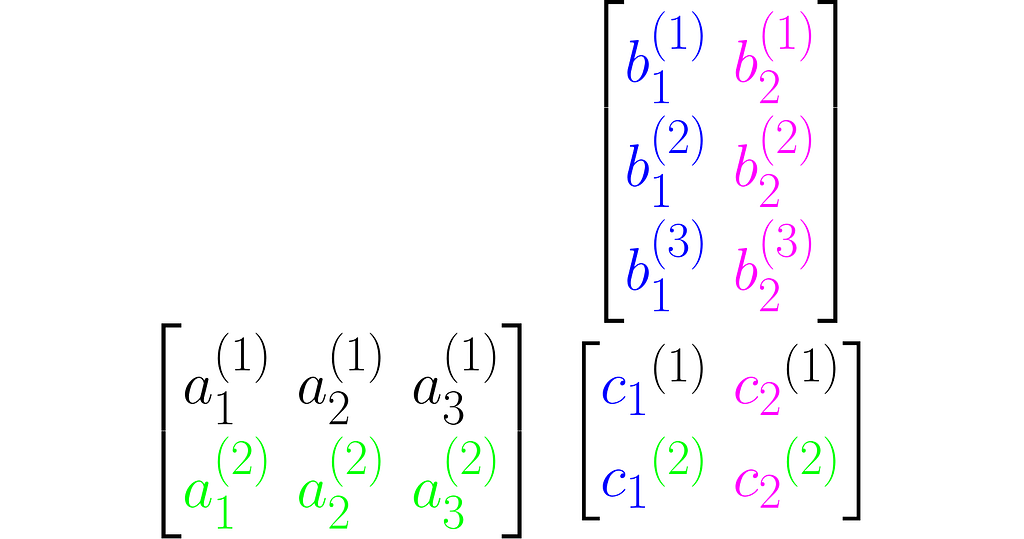
where cᵢ⁽ʲ ⁾ is the scalar product of the i-th column of the matrix B and the j-th row of matrix A:
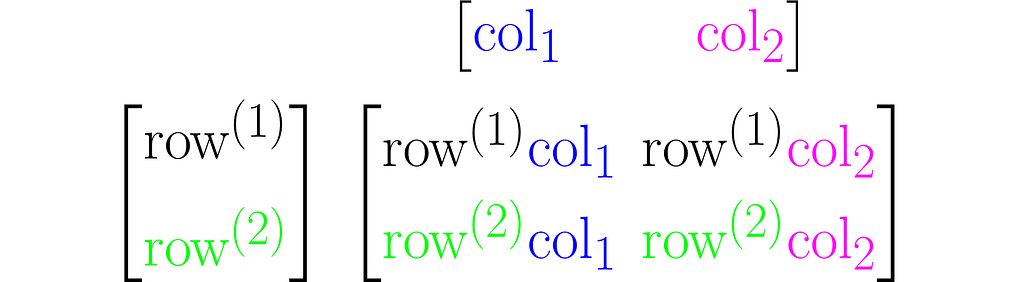
Note that this definition of multiplication requires the number of rows of the left matrix to match the number of columns of the right matrix. In other words, the inner dimensions of the matrices must match.
Make sure you can manually multiply matrices with arbitrary entries. You can use the following code to check the result or to practice multiplying matrices.
import numpy as np
# Matrices to be multiplied
A = [
[ 1, 0, 2],
[-2, 1, 1]
]
B = [
[ 0, 3, 1],
[-3, 1, 1],
[-2, 2, 1]
]
# Convert to numpy array
A = np.array(A)
B = np.array(B)
# Multiply A by B (if possible)
try:
C = A @ B
print(f'A B = n{C}n')
except:
print("""ValueError:
The number of rows in matrix A does not match
the number of columns in matrix B
""")
# and in the reverse order, B by A (if possible)
try:
D = B @ A
print(f'B A =n{D}')
except:
print("""ValueError:
The number of rows in matrix B does not match
the number of columns in matrix A
""")
A B = [[-4 7] [-5 -3]] B A = [[-6 3 3] [-5 1 -5] [-6 2 -2]]
3. Matrix-vector multiplication
In this section, I will explain the effect of matrix multiplication on vectors. The vector x is multiplied by the matrix A, producing a new vector y:
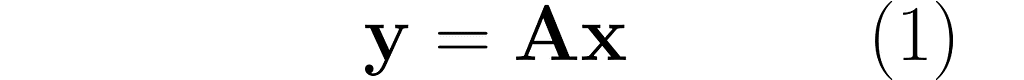
This is a common operation in data science, as it enables a linear transformation of data. The use of matrices to represent linear transformations is highly advantageous, as you will soon see in the following examples.
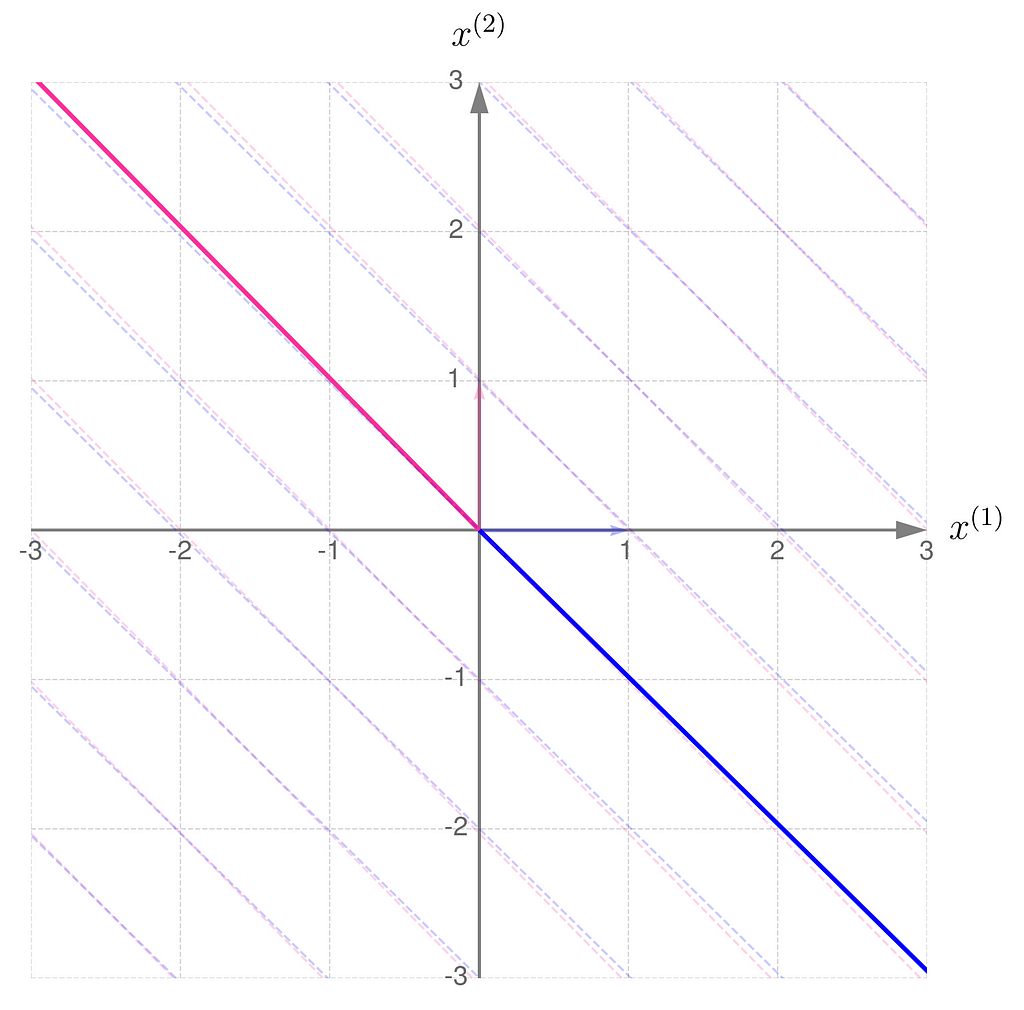
Below, you can see your grid space and your standard basis vectors: blue for the x⁽¹⁾ direction and magenta for the x⁽²⁾ direction.
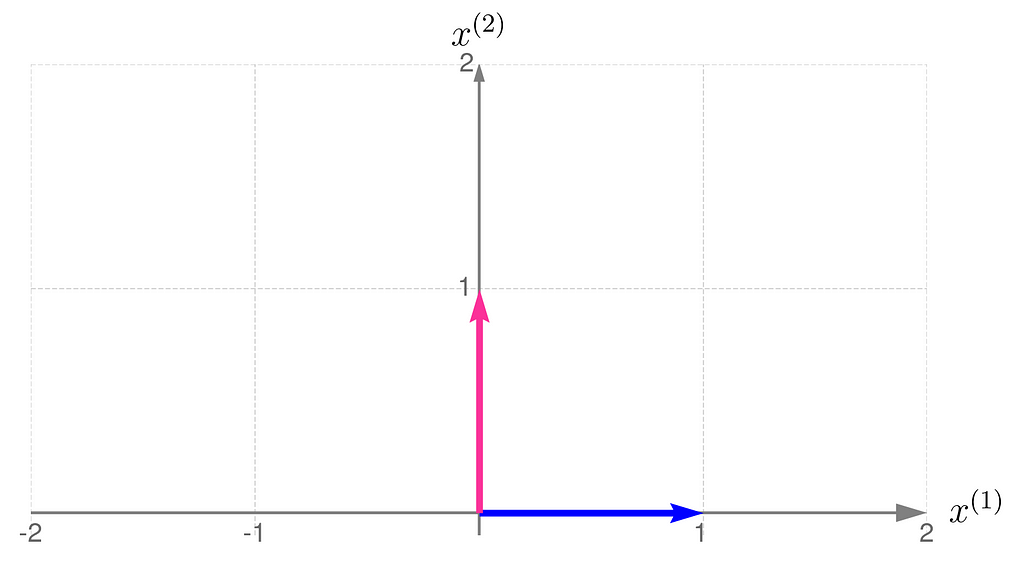
A good starting point is to work with transformations that map two-dimensional vectors x into two-dimensional vectors y in the same grid space.
Describing the desired transformation is a simple trick. You just need to say how the coordinates of the basis vectors change after the transformation and use these new coordinates as the columns of the matrix A.
As an example, consider a linear transformation that produces the effect illustrated below. The standard basis vectors are drawn lightly, while the transformed vectors are shown more clearly.
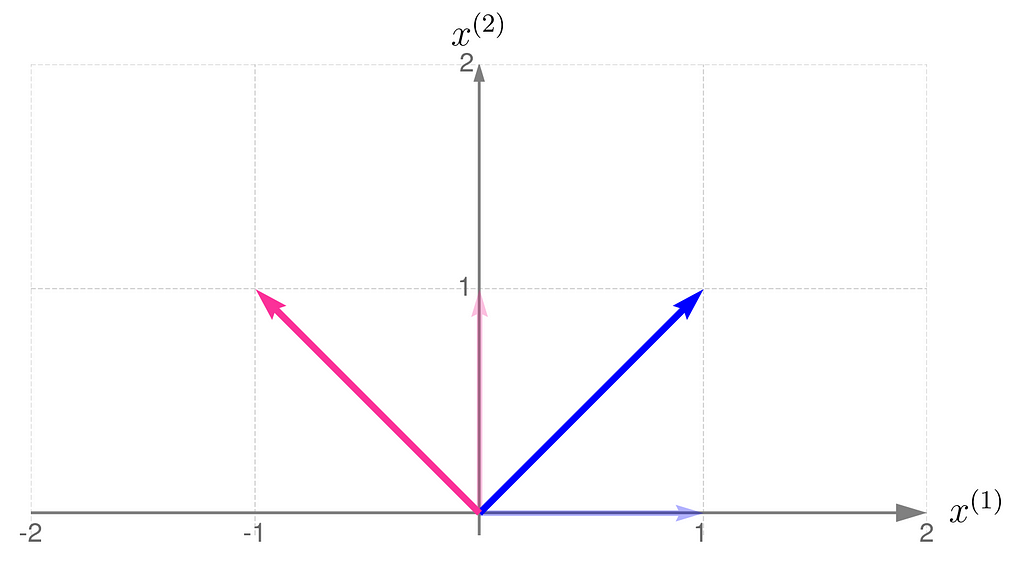
From the comparison of the basis vectors before and after the transformation, you can observe that the transformation involves a 45-degree counterclockwise rotation about the origin, along with an elongation of the vectors.
This effect can be achieved using the matrix A, composed as follows:
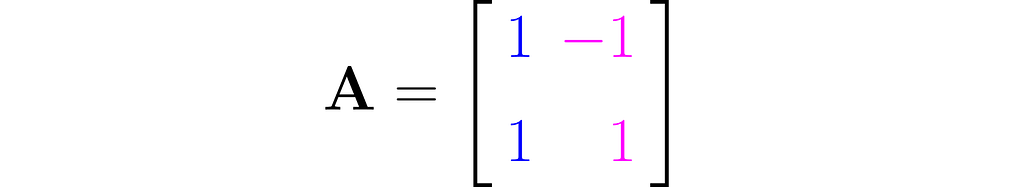
The first column of the matrix contains the coordinates of the first basis vector after the transformation, and the second column contains those of the second basis vector.
The equation (1) then takes the form

Let’s take two example points x₁and x₂ :
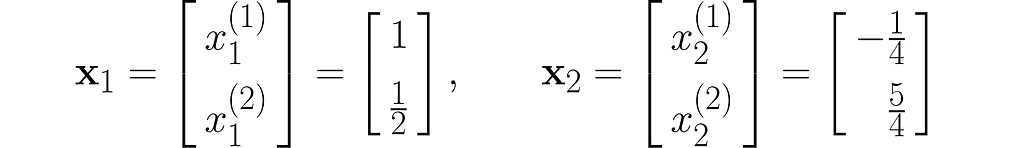
and transform them into the vectors y₁ and y₂ :
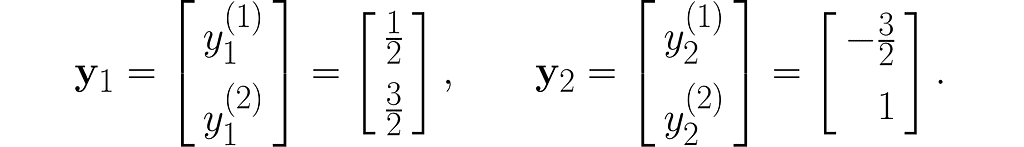
I encourage you to do these calculations by hand first, and then switch to using a program like this:
import numpy as np
# Transformation matrix
A = np.array([
[1, -1],
[1, 1]
])
# Points (vectors) to be transformed using matrix A
points = [
np.array([1, 1/2]),
np.array([-1/4, 5/4])
]
# Print out the transformed points (vectors)
for i, x in enumerate(points):
y = A @ x
print(f'y_{i} = {y}')
y_0 = [0.5 1.5] y_1 = [-1.5 1. ]
The plot below shows the results.
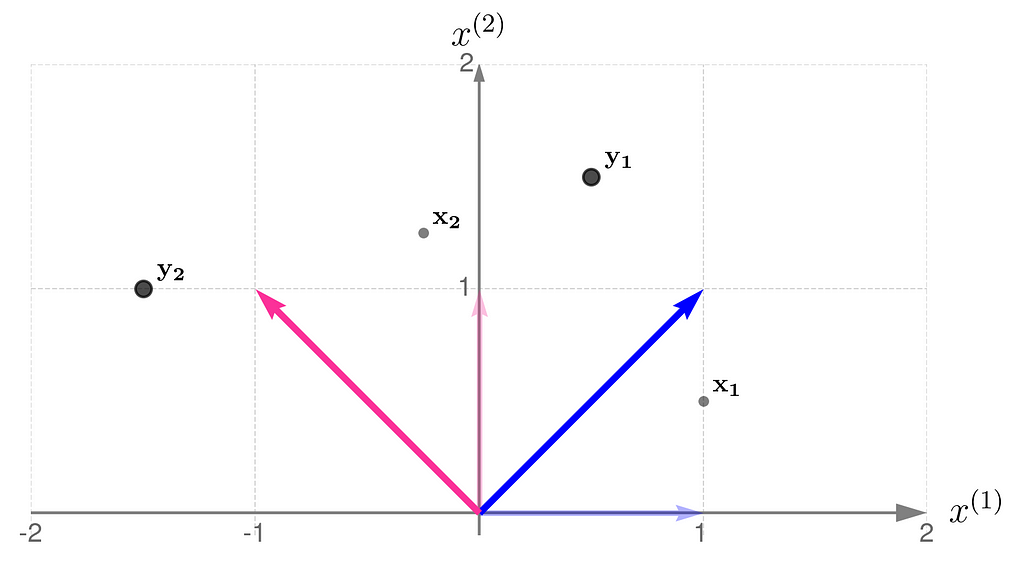
The x points are gray and smaller, while their transformed counterparts y have black edges and are bigger. If you’d prefer to think of these points as arrowheads, here’s the corresponding illustration:
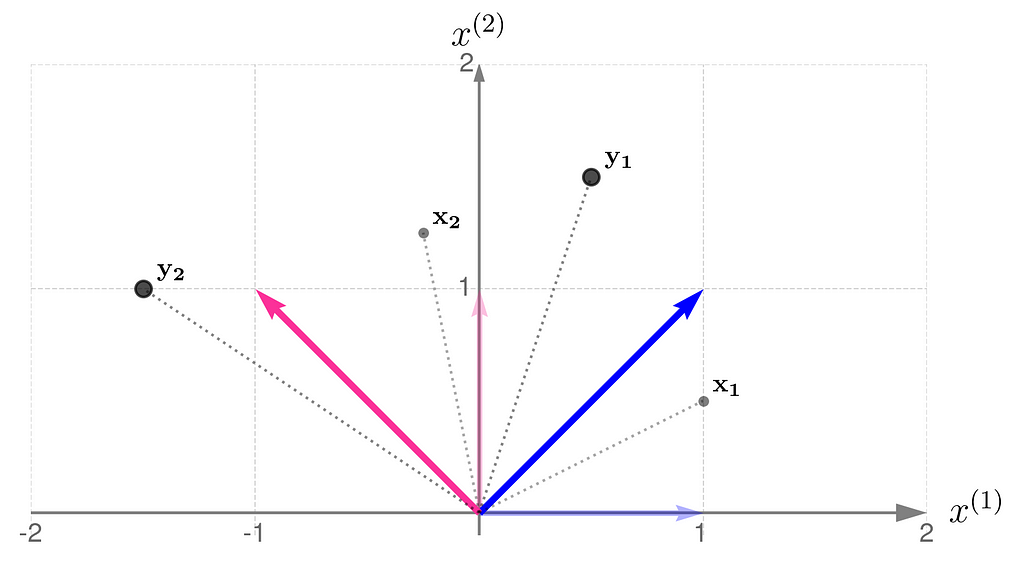
Now you can see more clearly that the points have been rotated around the origin and pushed a little away.
Let’s examine another matrix:
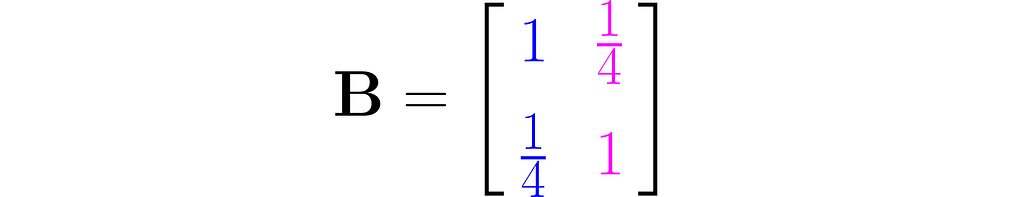
and see how the transformation
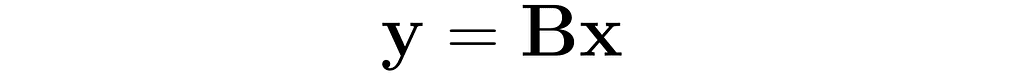
affects the points on the grid lines:
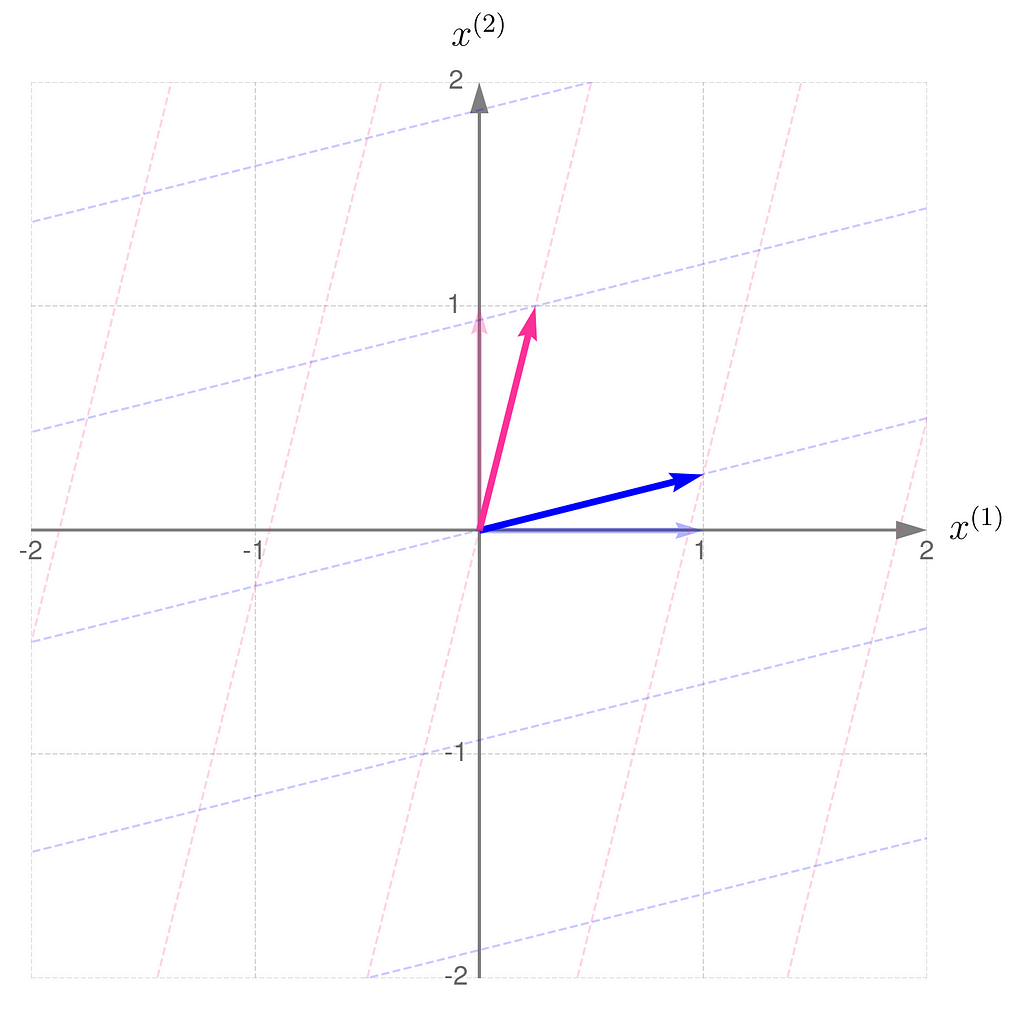
Compare the result with that obtained using B/2, which corresponds to dividing all elements of the matrix B by 2:
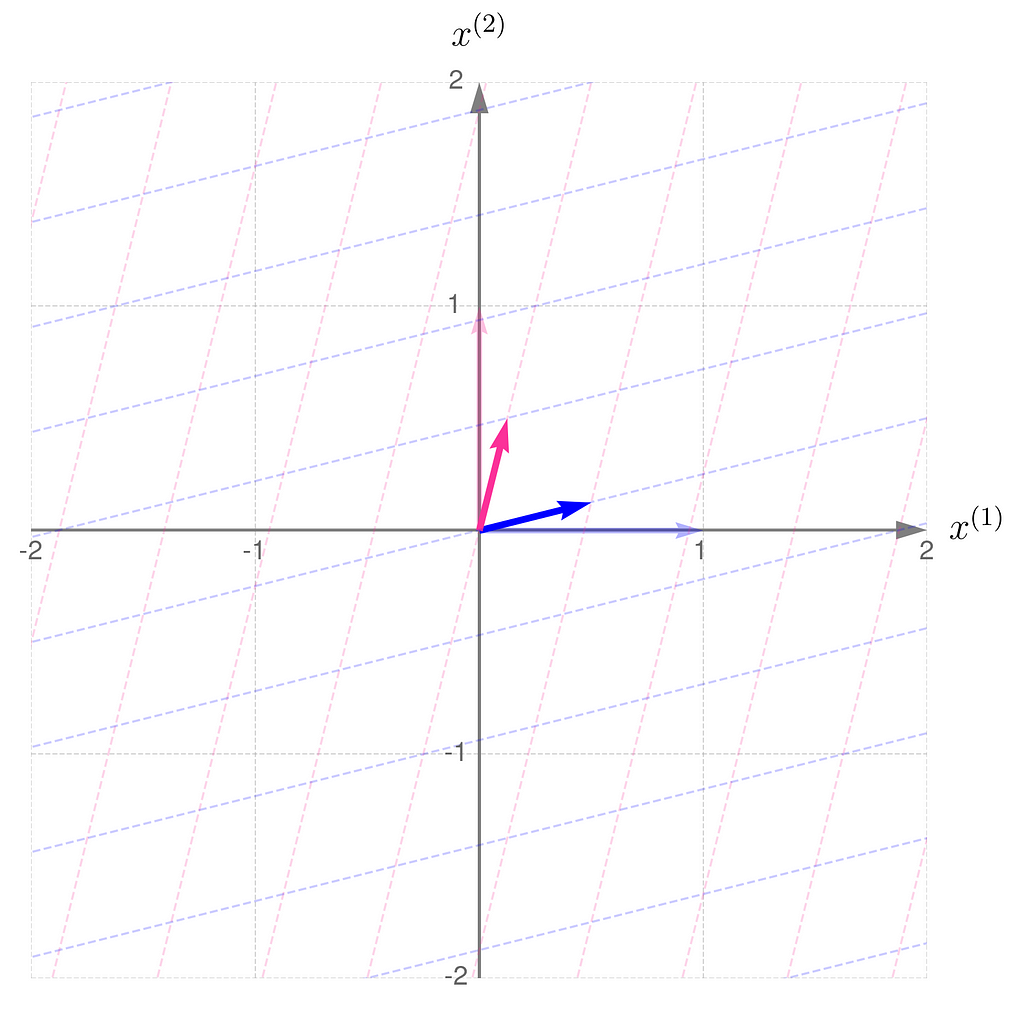
In general, a linear transformation:
- ensures that straight lines remain straight,
- keeps parallel lines parallel,
- scales the distances between them by a uniform factor.
To keep things concise, I’ll use ‘transformation A‘ throughout the text instead of the full phrase ‘transformation represented by matrix A’.
Let’s return to the matrix
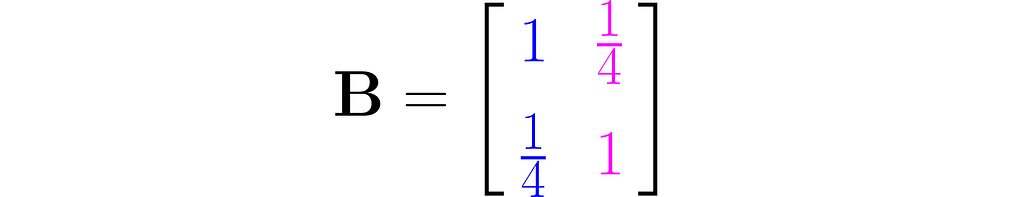
and apply the transformation to a few sample points.
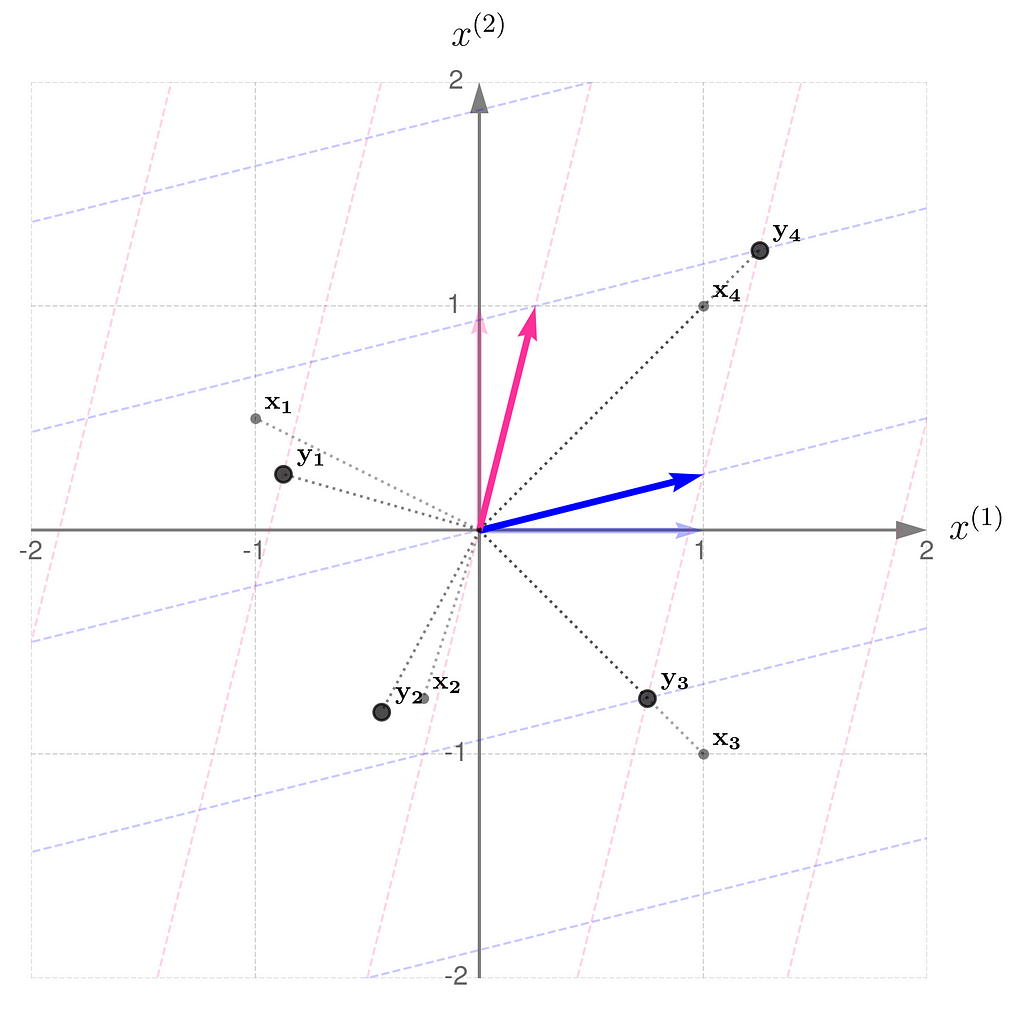
Notice the following:
- point x₁ has been rotated counterclockwise and brought closer to the origin,
- point x₂, on the other hand, has been rotated clockwise and pushed away from the origin,
- point x₃ has only been scaled down, meaning it’s moved closer to the origin while keeping its direction,
- point x₄ has undergone a similar transformation, but has been scaled up.
The transformation compresses in the x⁽¹⁾-direction and stretches in the x⁽²⁾-direction. You can think of the grid lines as behaving like an accordion.
Directions such as those represented by the vectors x₃ and x₄ play an important role in machine learning, but that’s a story for another time.
For now, we can call them eigen-directions, because vectors along these directions might only be scaled by the transformation, without being rotated. Every transformation, except for rotations, has its own set of eigen-directions.
4. Transposition
Recall that the transformation matrix is constructed by stacking the transformed basis vectors in columns. Perhaps you’d like to see what happens if we swap the rows and columns afterwards (the transposition).
Let us take, for example, the matrix
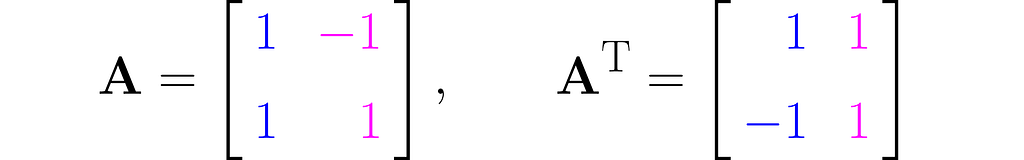
where Aᵀ stands for the transposed matrix.
From a geometric perspective, the coordinates of the first new basis vector come from the first coordinates of all the old basis vectors, the second from the second coordinates, and so on.
In NumPy, it’s as simple as that:
import numpy as np
A = np.array([
[1, -1],
[1 , 1]
])
print(f'A transposed:n{A.T}')
A transposed: [[ 1 1] [-1 1]]
I must disappoint you now, as I cannot provide a simple rule that expresses the relationship between the transformations A and Aᵀ in just a few words.
Instead, let me show you a property shared by both the original and transposed transformations, which will come in handy later.
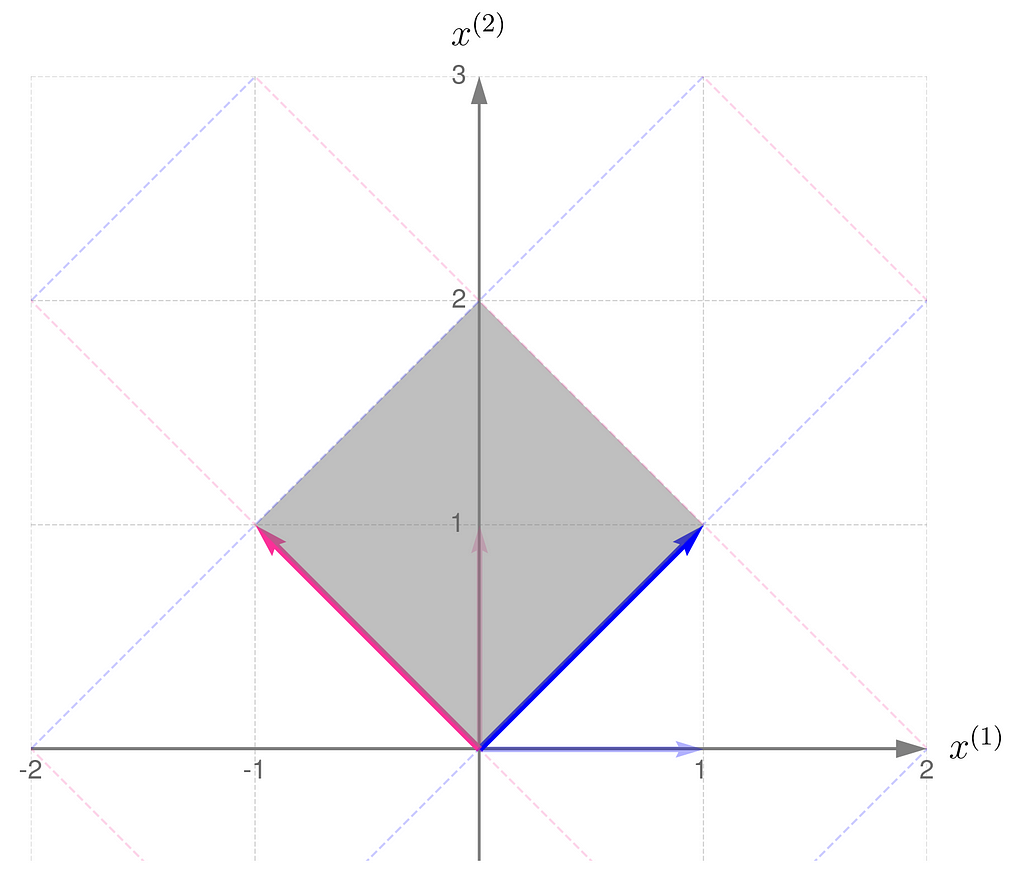
Here is the geometric interpretation of the transformation represented by the matrix A. The area shaded in gray is called the parallelogram.
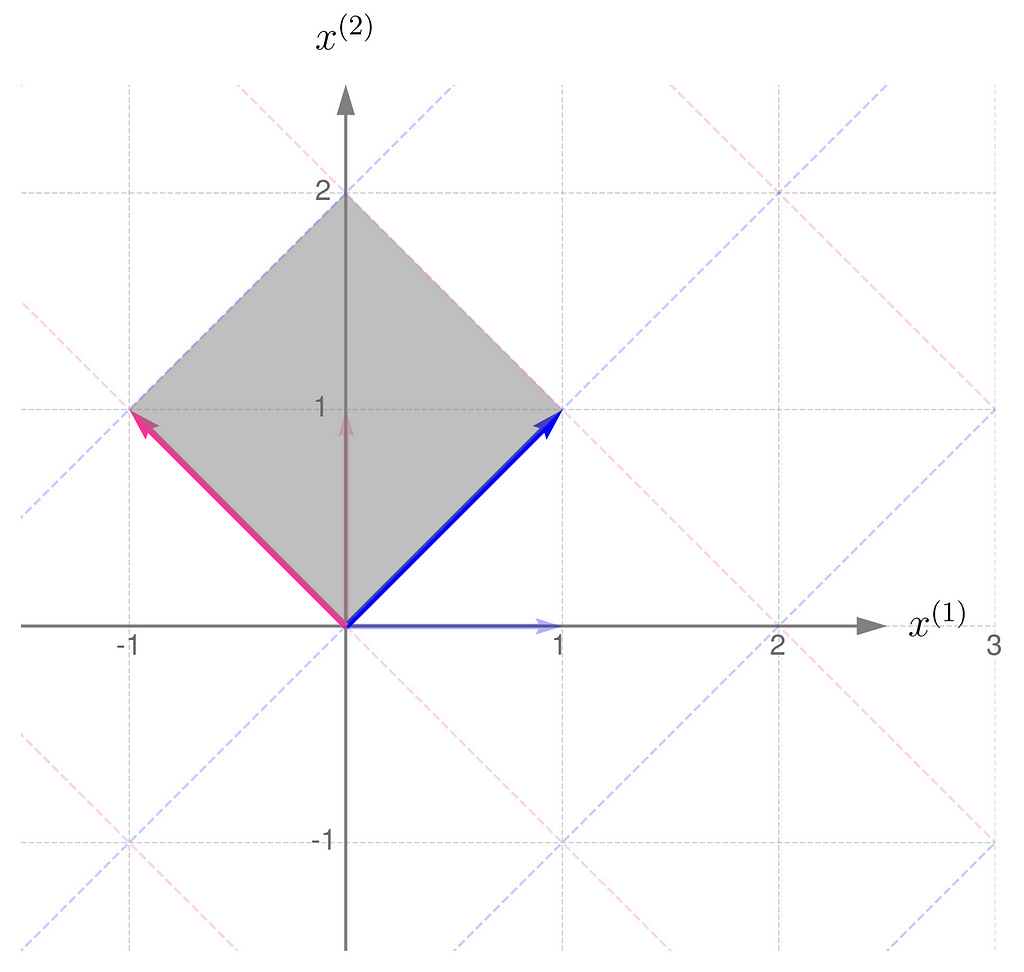
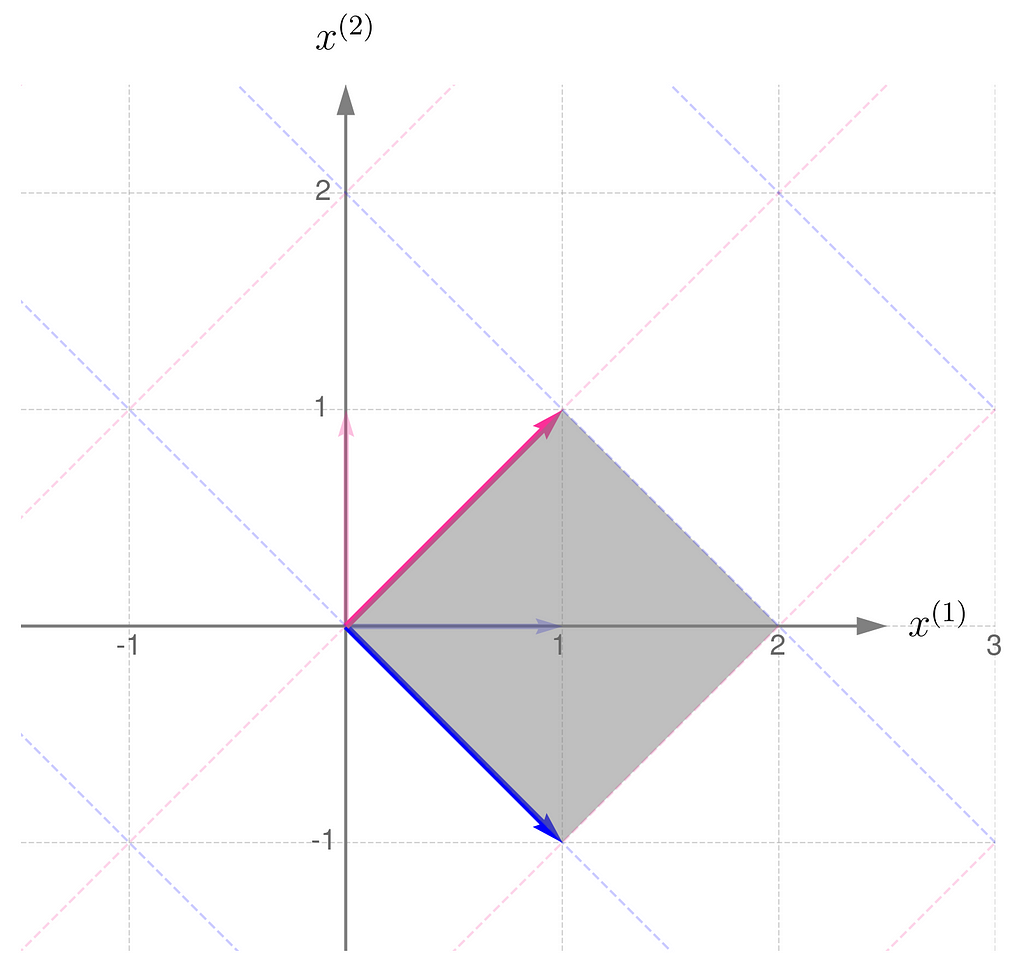
Compare this with the transformation obtained by applying the matrix Aᵀ:
Now, let us consider another transformation that applies entirely different scales to the unit vectors:

The parallelogram associated with the matrix B is much narrower now:
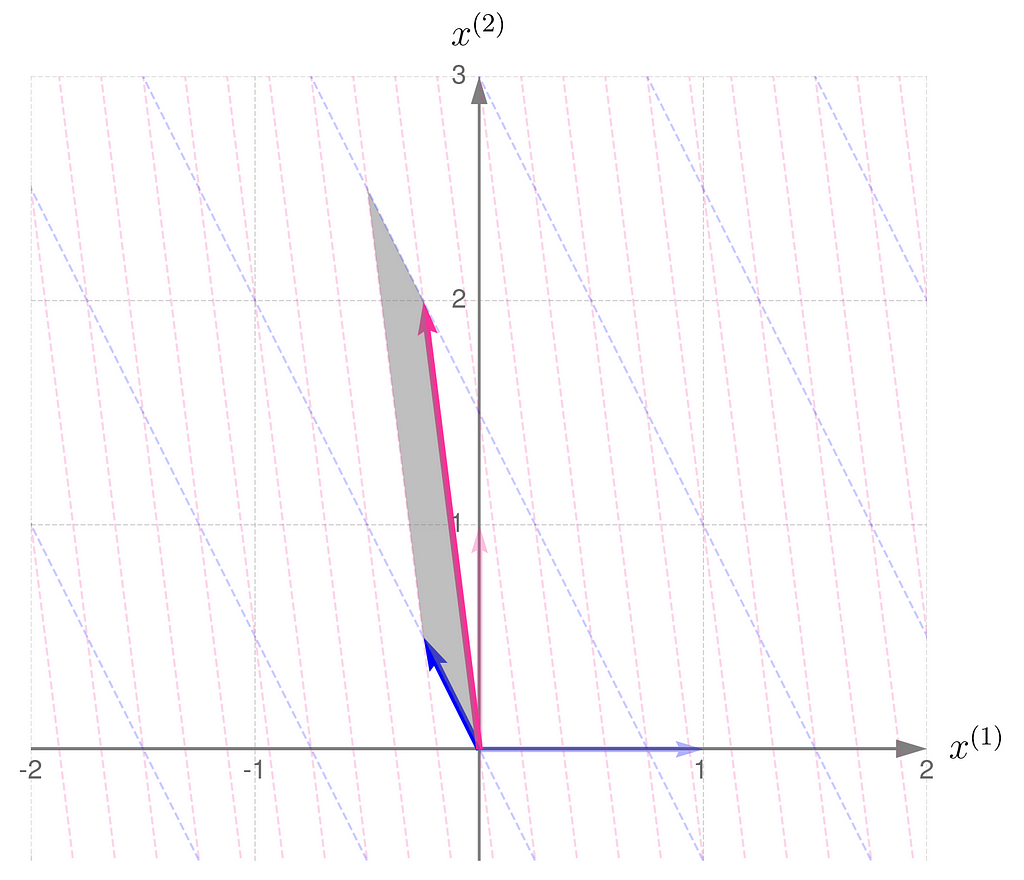
but it turns out that it is the same size as that for the matrix Bᵀ:
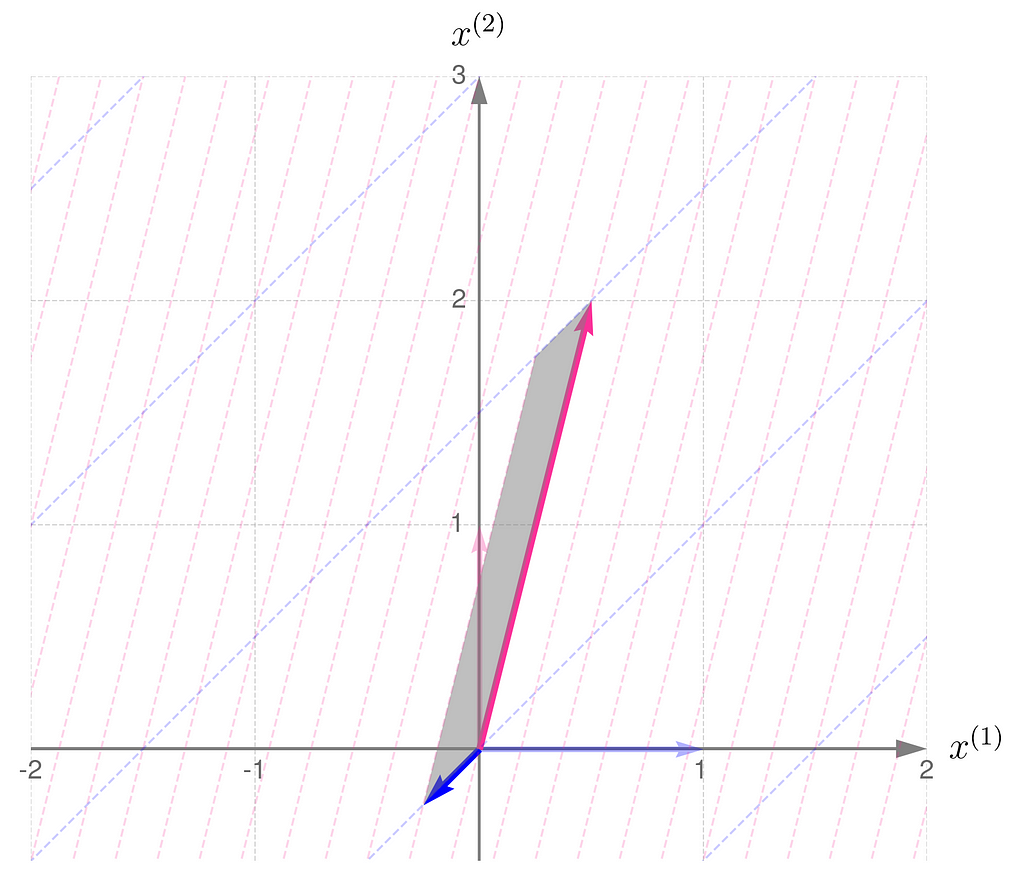
Let me put it this way: you have a set of numbers to assign to the components of your vectors. If you assign a larger number to one component, you’ll need to use smaller numbers for the others. In other words, the total length of the vectors that make up the parallelogram stays the same. I know this reasoning is a bit vague, so if you’re looking for more rigorous proofs, check the literature in the references section.
And here’s the kicker at the end of this section: the area of the parallelograms can be found by calculating the determinant of the matrix. What’s more, the determinant of the matrix and its transpose are identical.
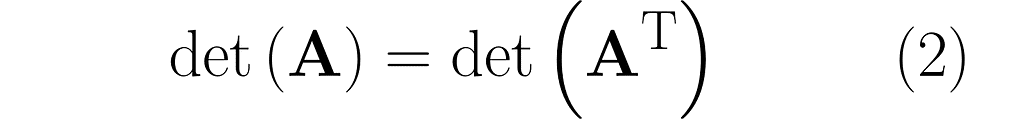
More on the determinant in the upcoming sections.
5. Composition of transformations
You can apply a sequence of transformations — for example, start by applying A to the vector x, and then pass the result through B. This can be done by first multiplying the vector x by the matrix A, and then multiplying the result by the matrix B:
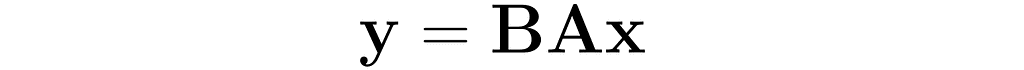
You can multiply the matrices B and A to obtain the matrix C for further use:
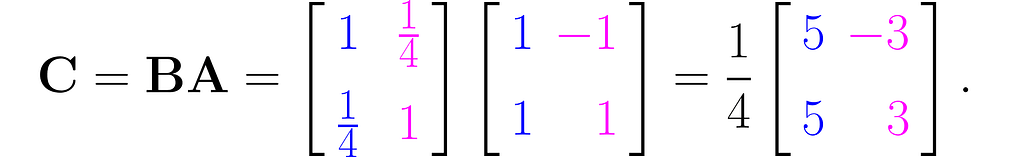
This is the effect of the transformation represented by the matrix C:
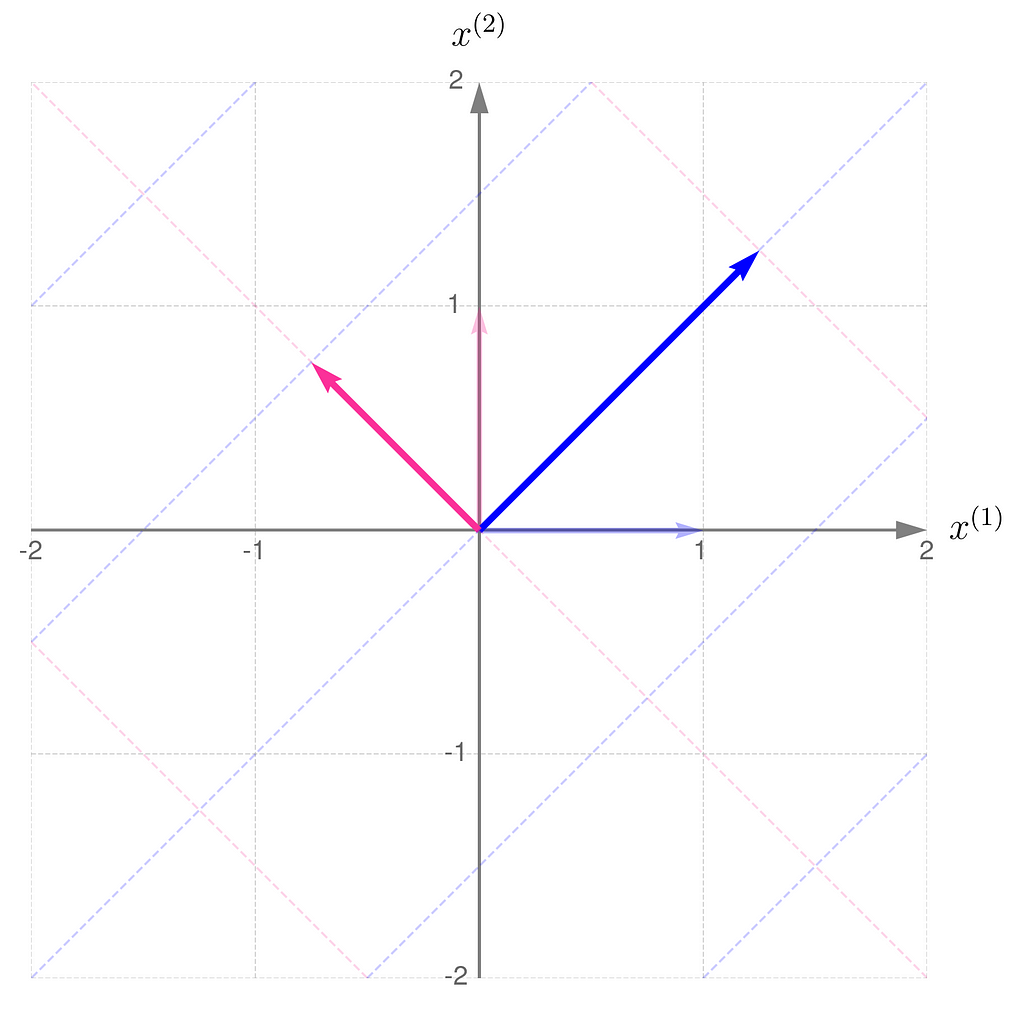
You can perform the transformations in reverse order: first apply B, then apply A:

Let D represent the sequence of multiplications performed in this order:

And this is how it affects the grid lines:
So, you can see for yourself that the order of matrix multiplication matters.
There’s a cool property with the transpose of a composite transformation. Check out what happens when we multiply A by B:
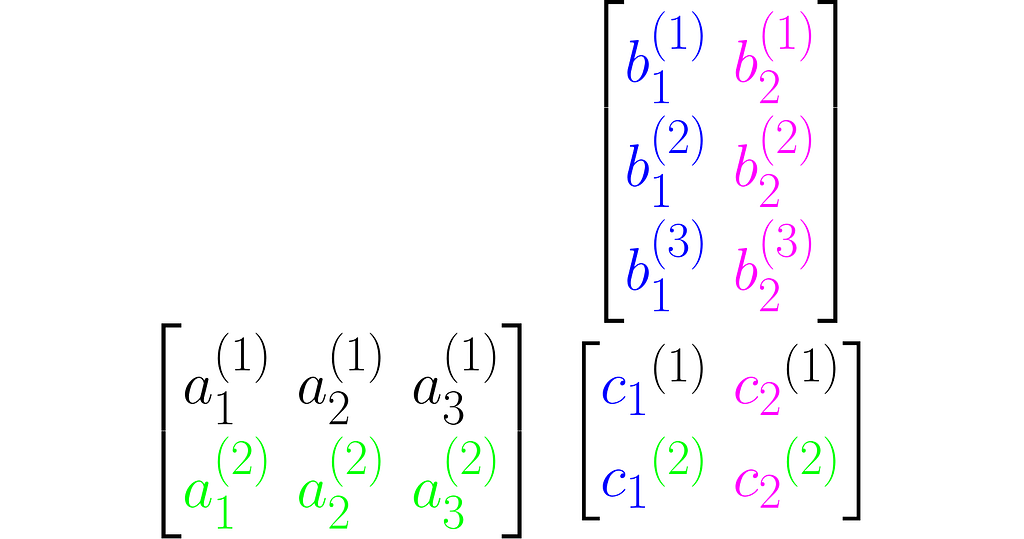
and then transpose the result, which means we’ll apply (AB)ᵀ:
You can easily extend this observation to the following rule:
To finish off this section, consider the inverse problem: is it possible to recover matrices A and B given only C = AB?
This is matrix factorization, which, as you might expect, doesn’t have a unique solution. Matrix factorization is a powerful technique that can provide insight into transformations, as they may be expressed as a composition of simpler, elementary transformations. But that’s a topic for another time.
6. Inverse transformation
You can easily construct a matrix representing a do-nothing transformation that leaves the standard basis vectors unchanged:
It is commonly referred to as the identity matrix.
Take a matrix A and consider the transformation that undoes its effects. The matrix representing this transformation is A⁻¹. Specifically, when applied after or before A, it yields the identity matrix I:
There are many resources that explain how to calculate the inverse by hand. I recommend learning Gauss-Jordan method because it involves simple row manipulations on the augmented matrix. At each step, you can swap two rows, rescale any row, or add to a selected row a weighted sum of the remaining rows.
Take the following matrix as an example for hand calculations:
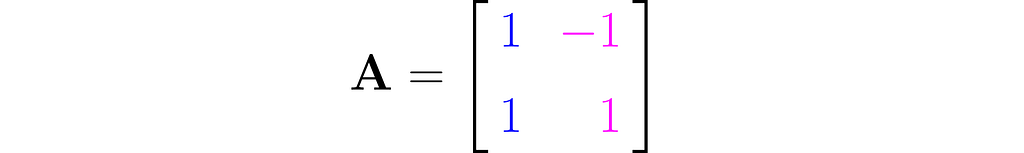
You should get the inverse matrix:
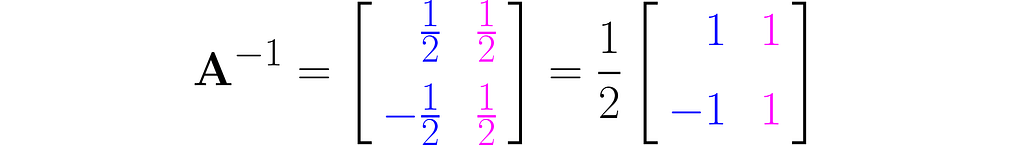
Verify by hand that equation (4) holds. You can also do this in NumPy.
import numpy as np
A = np.array([
[1, -1],
[1 , 1]
])
print(f'Inverse of A:n{np.linalg.inv(A)}')
Inverse of A: [[ 0.5 0.5] [-0.5 0.5]]
Take a look at how the two transformations differ in the illustrations below.
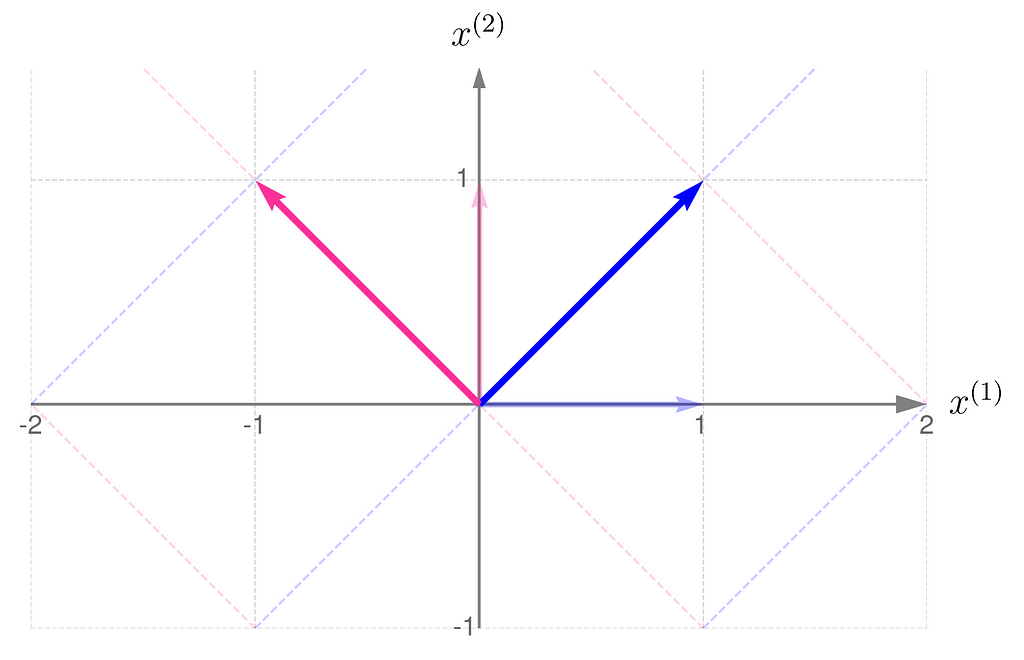
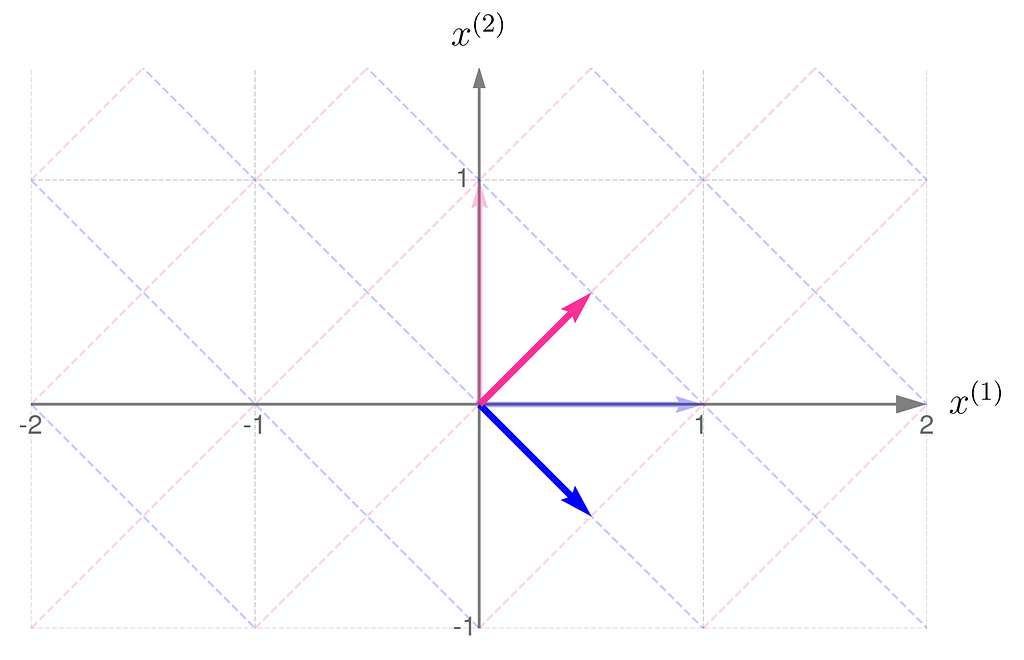
At first glance, it’s not obvious that one transformation reverses the effects of the other.
However, in these plots, you might notice a fascinating and far-reaching connection between the transformation and its inverse.
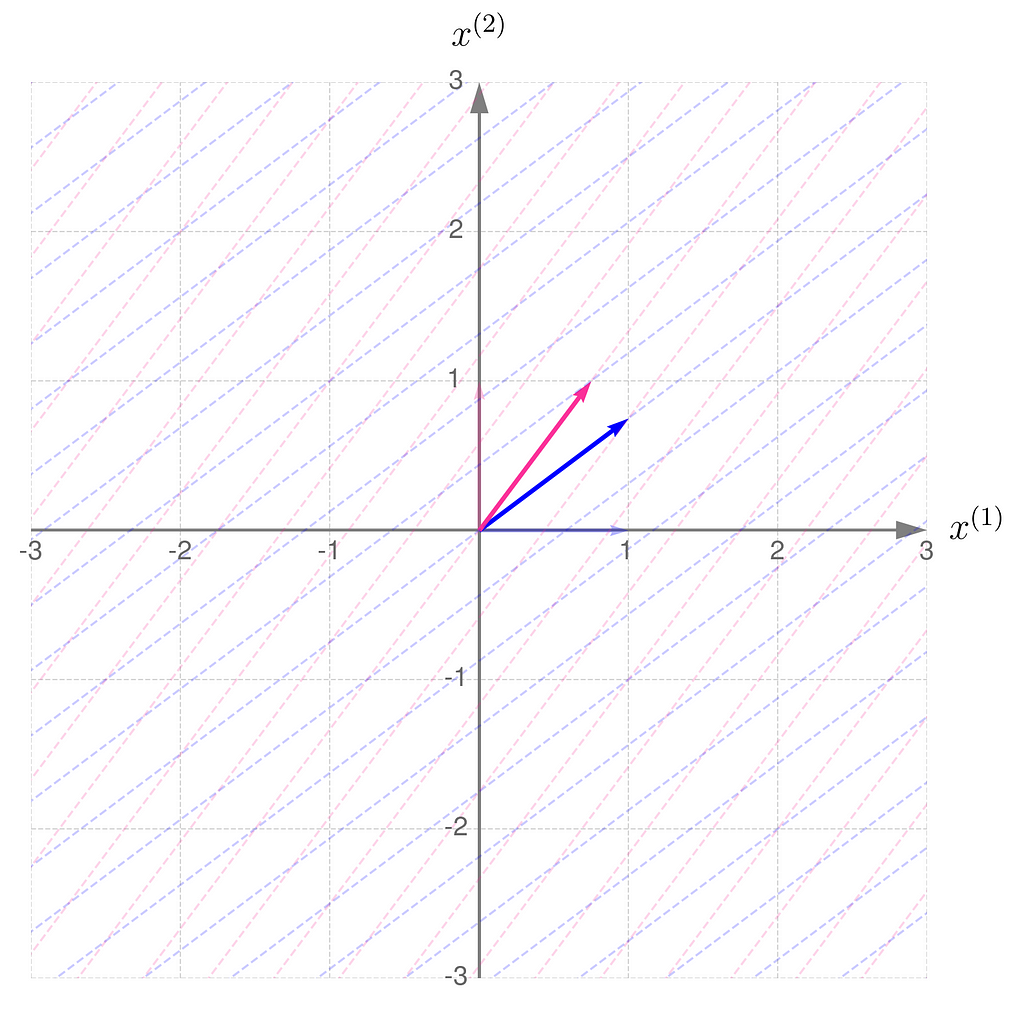
Take a close look at the first illustration, which shows the effect of transformation A on the basis vectors. The original unit vectors are depicted semi-transparently, while their transformed counterparts, resulting from multiplication by matrix A, are drawn clearly and solidly. Now, imagine that these newly drawn vectors are the basis vectors you use to describe the space, and you perceive the original space from their perspective. Then, the original basis vectors will appear smaller and, secondly, will be oriented towards the east. And this is exactly what the second illustration shows, demonstrating the effect of the transformation A⁻¹.
This is a preview of an upcoming topic I’ll cover in the next article about using matrices to represent different perspectives on data.
All of this sounds great, but there’s a catch: some transformations can’t be reversed.
7. Non-invertible transformations
The workhorse of the next experiment will be the matrix with 1s on the diagonal and b on the antidiagonal:
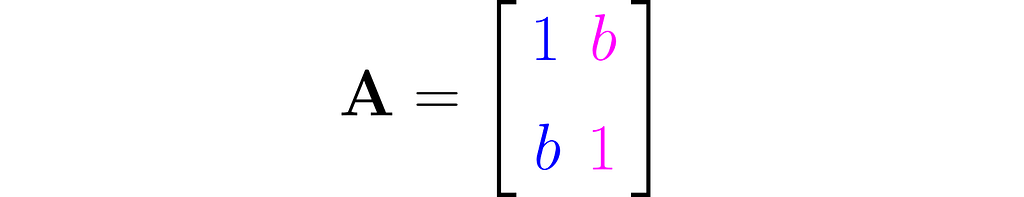
where b is a fraction in the interval (0, 1). This matrix is, by definition, symmetrical, as it happens to be identical to its own transpose: A=Aᵀ, but I’m just mentioning this by the way; it’s not particularly relevant here.
Invert this matrix using the Gauss-Jordan method, and you will get the following:
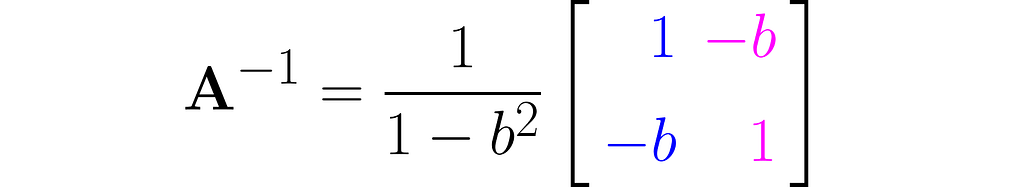
You can easily find online the rules for calculating the determinant of 2×2 matrices, which will give
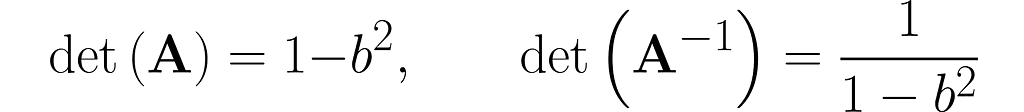
This is no coincidence. In general, it holds that
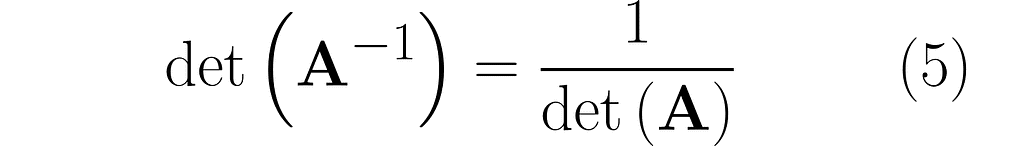
Notice that when b = 0, the two matrices are identical. This is no surprise, as A reduces to the identity matrix I.
Things get tricky when b = 1, as the det(A) = 0 and det(A⁻¹) becomes infinite. As a result, A⁻¹ does not exist for a matrix A consisting entirely of 1s. In algebra classes, teachers often warn you about a zero determinant. However, when we consider where the matrix comes from, it becomes apparent that an infinite determinant can also occur, resulting in a fatal error. Anyway,
a zero determinant means the transformation is non-ivertible.
Now, the stage is set for experiments with different values of b. We’ve just seen how calculations fail at the limits, so let’s now visually investigate what happens as we carefully approach them.
We start with b = ½ and end up near 1.
Step 1)
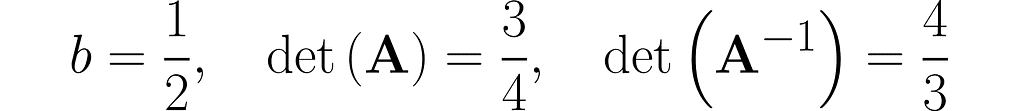
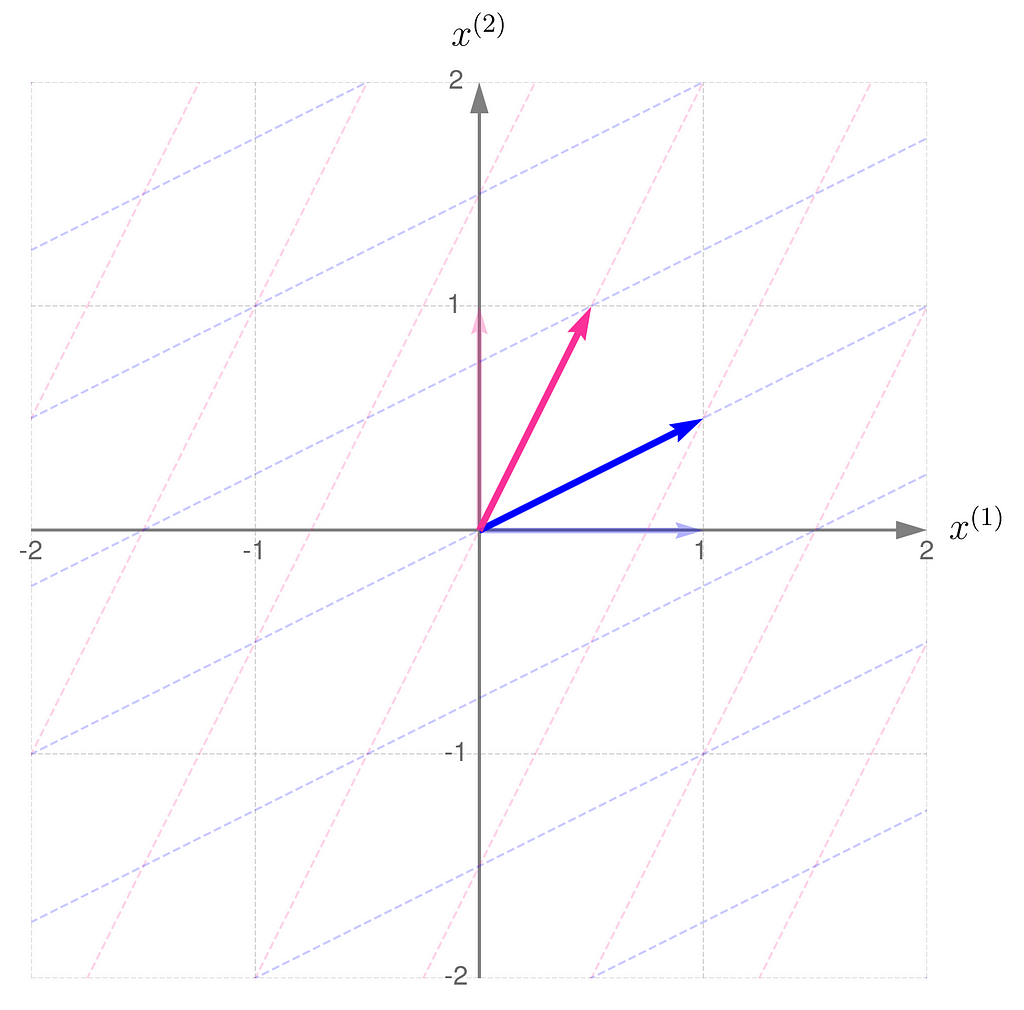
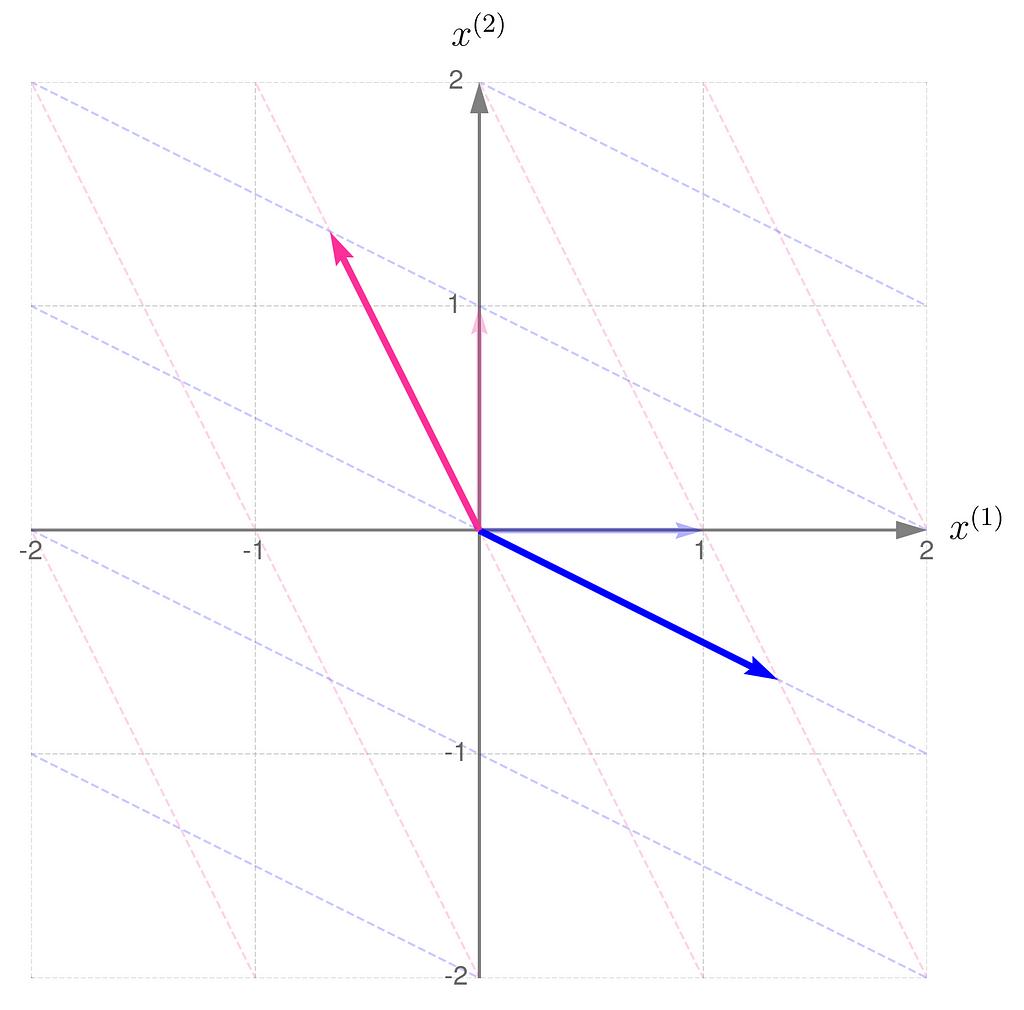
Step 2)
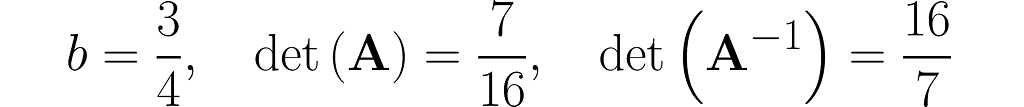
Recall that the determinant of the matrix representing the transformation corresponds to the area of the parallelogram formed by the transformed basis vectors.
This is in line with the illustrations: the smaller the area of the parallelogram for transformation A, the larger it becomes for transformation A⁻¹. What follows is: the narrower the basis for transformation A, the wider it is for its inverse. Note also that I had to extend the range on the axes because the basis vectors for transformation A are getting longer.
By the way, notice that
the transformation A has the same eigen-directions as A⁻¹.
Step 3) Almost there…
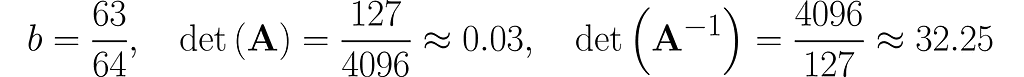
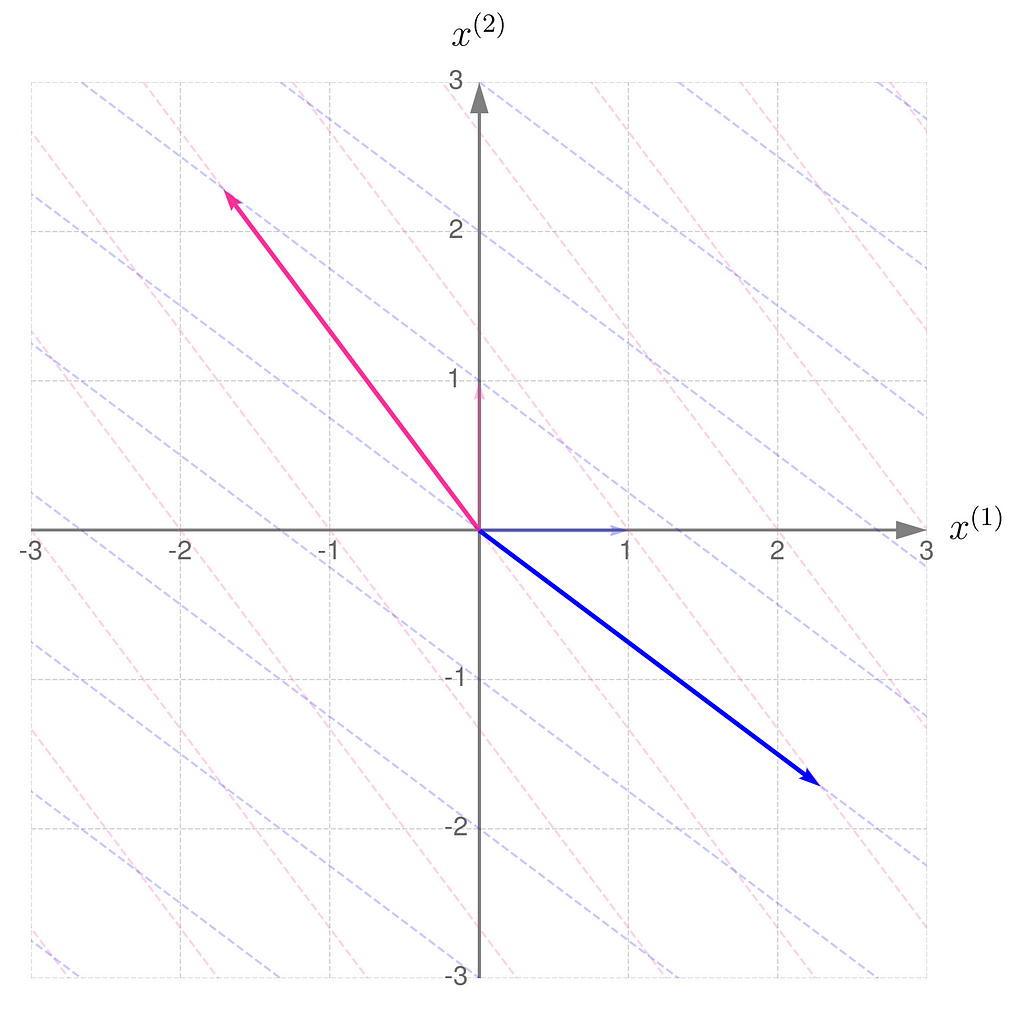
The gridlines are squeezed so much that they almost overlap, which eventually happens when b hits 1. The basis vectors of are stretched so far that they go beyond the axis limits. When b reaches exactly 1, both basis vectors lie on the same line.
Having seen the previous illustrations, you’re now ready to guess the effect of applying a non-invertible transformation to the vectors. Take a moment to think it through first, then either try running a computational experiment or check out the results I’ve provided below.
.
.
.
Think of it this way.
When the basis vectors are not parallel, meaning they form an angle other than 0 or 180 degrees, you can use them to address any point on the entire plane (mathematicians say that the vectors span the plane). Otherwise, the entire plane can no longer be spanned, and only points along the line covered by the basis vectors can be addressed.
.
.
.
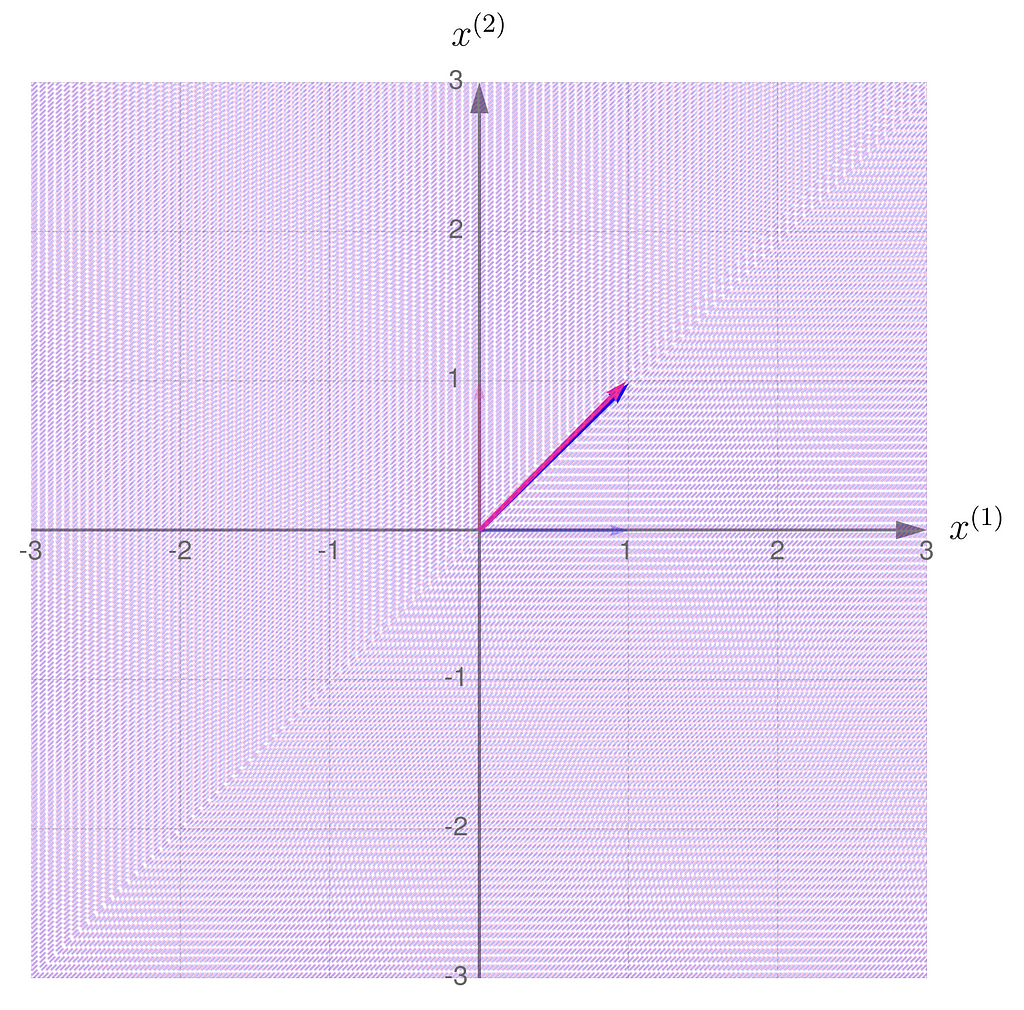
This is what it looks like when you apply the non-invertible transformation to randomly selected points:
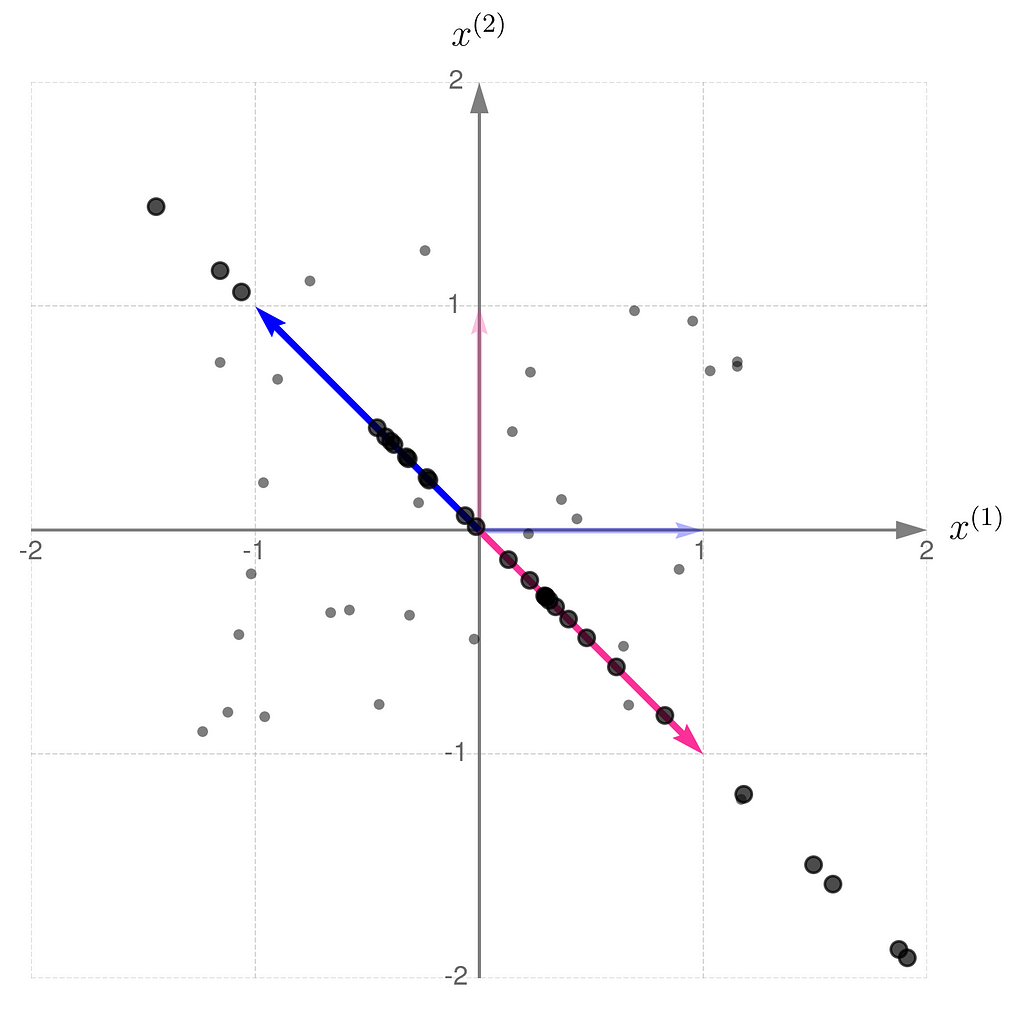
A consequence of applying a non-invertible transformation is that the two-dimensional space collapses to a one-dimensional subspace. After the transformation, it is no longer possible to uniquely recover the original coordinates of the points.
Take a look at the entries of matrix A. When b = 1, both columns (and rows) are identical, implying that the transformation matrix effectively behaves as if it were a 1 by 2 matrix, mapping two-dimensional vectors to a scalar.
You can easily verify that the problem would be the same if one row were a multiple of the other. This can be further generalized for matrices of any dimensions: if any row can be expressed as a weighted sum (linear combination) of the others, it implies that a dimension collapses. The reason is that such a vector lies within the space spanned by the other vectors, so it does not provide any additional ability to address points beyond those that can already be addressed. You may consider this vector redundant.
From section 4 on transposition, we can infer that if there are redundant rows, there must be an equal number of redundant columns.
8. Determinant
You might now ask if there’s a non-geometrical way to verify whether the columns or rows of the matrix are redundant.
Recall the parallelograms from Section 4 and the scalar quantity known as the determinant. I mentioned that
the determinant of a matrix indicates how the area of a unit parallelogram changes under the transformation.
The exact definition of the determinant is somewhat tricky, but as you’ve already seen, its graphical interpretation should not cause any problems.
I will demonstrate the behavior of two transformations represented by matrices:
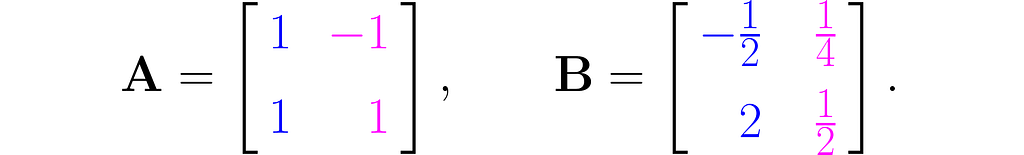
The magnitude of the determinant indicates how much the transformation stretches (if greater than 1) or shrinks (if less than 1) the space overall. While the transformation may stretch along one direction and compress along another, the overall effect is given by the value of the determinant.
Also, a negative determinant indicates a reflection; note that matrix B reverses the order of the basis vectors.
A parallelogram with zero area corresponds to a transformation that collapses a dimension, meaning the determinant can be used to test for redundancy in the basis vectors of a matrix.
Since the determinant measures the area of a parallelogram under a transformation, we can apply it to a sequence of transformations. If det(A) and det(B) represent the scaling factors of unit areas for transformations A and B, then the scaling factor for the unit area after applying both transformations sequentially, that is, AB, is equal to det(AB). As both transformations act independently and one after the other, the total effect is given by det(AB) = det(A) det(B). Substituting matrix A⁻¹ for matrix B and noting that det(I) = 1 leads to equation (5) introduced in the previous section.
Here’s how you can calculate the determinant using NumPy:
import numpy as np
A = np.array([
[-1/2, 1/4],
[2, 1/2]
])
print(f'det(A) = {np.linalg.det(A)}')
det(A) = -0.75
9. Non-square matrices
Until now, we’ve focused on square matrices, and you’ve developed a geometric intuition of the transformations they represent. Now is a great time to expand these skills to matrices with any number of rows and columns.
Wide matrices
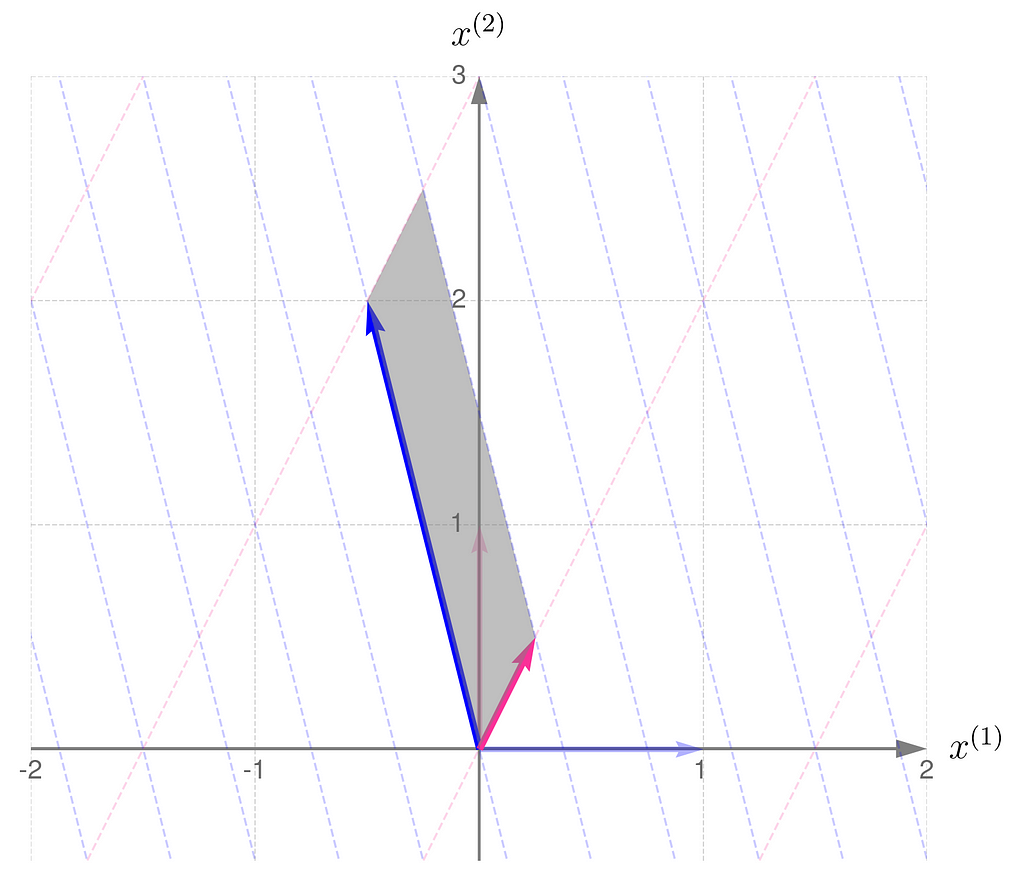
This is an example of a wide matrix, which has more columns than rows:
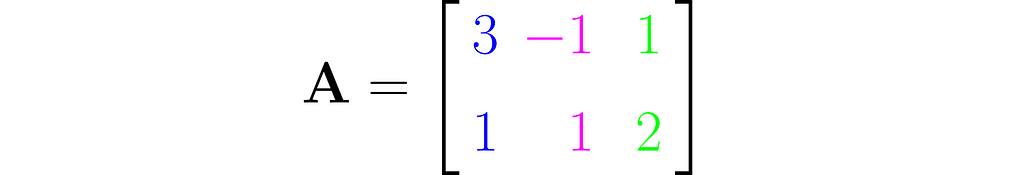
From the perspective of equation (1), y = Ax, it maps three-dimensional vectors x to two-dimensional vectors y.
In such a case, one column can always be expressed as a multiple of another or as a weighted sum of the others. For example, the third column here equals 3/4 times the first column plus 5/4 times the second.
Once the vector x has been transformed into y, it’s no longer possible to reconstruct the original x from y. We say that the transformation reduces the dimensionality of the input data. These types of transformations are very important in machine learning.
Sometimes, a wide matrix disguises itself as a square matrix, but you can reveal it by checking whether its determinant is zero. We’ve had this situation before, remember?
We can use the matrix A to create two different square matrices. Try deriving the following result yourself:
and also determinants (I recommend simplified formulas for working with 2×2 and 3×3 matrices):
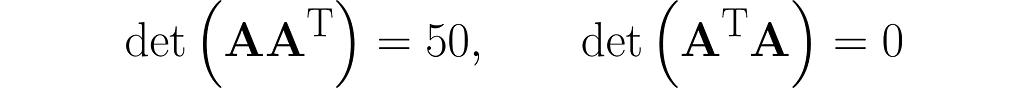
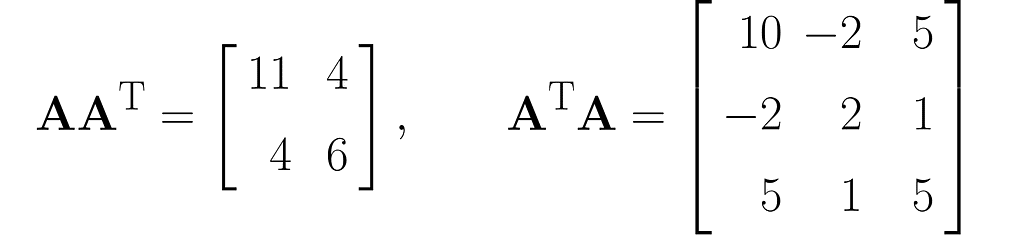
The matrix AᵀA is composed of the dot products of all possible pairs of columns from matrix A, some of which are definitely redundant, thereby transferring this redundancy to AᵀA.
Matrix AAᵀ, on the other hand, contains only the dot products of the rows of matrix A, which are fewer in number than the columns. Therefore, the vectors that make up matrix AAᵀ are most likely (though not entirely guaranteed) linearly independent, meaning that one vector cannot be expressed as a multiple of another or as a weighted sum of the others.
What would happen if you insisted on determining x from y, which was previously computed as y = Ax? You could left-multiply both sides by A⁻¹ to get equation A⁻¹y = A⁻¹Ax and, since A⁻¹A = I, obtain x = A⁻¹y. But this would fail from the very beginning, because matrix A⁻¹, being non-square, is certainly non-invertible (at least not in the sense that was previously introduced).
However, you can extend the original equation y = Ax to include a square matrix where it’s needed. You just need to left-multiply matrix Aᵀ on both sides of the equation, yielding Aᵀy = AᵀAx. On the right, we now have a square matrix AᵀA. Unfortunately, we’ve already seen that its determinant is zero, so it appears that we have once again failed to reconstruct x from y.
Tall matrices
Here is an example of a tall matrix
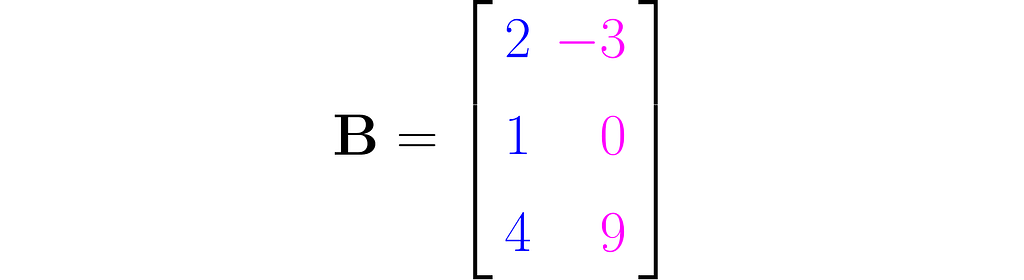
that maps two-dimensional vectors x into three-dimensional vectors y. I made a third row by simply squaring the entries of the first row. While this type of extension doesn’t add any new information to the data, it can surprisingly improve the performance of certain machine learning models.
You might think that, unlike wide matrices, tall matrices allow the reconstruction of the original x from y, where y = Bx, since no information is discarded — only added.
And you’d be right! Look at what happens when we left-multiply by matrix Bᵀ, just like we tried before, but without success: Bᵀy = BᵀBx. This time, matrix BᵀB is invertible, so we can left-multiply by its inverse:
(BᵀB)⁻¹Bᵀy = (BᵀB)⁻¹(BᵀB)x
and finally obtain:
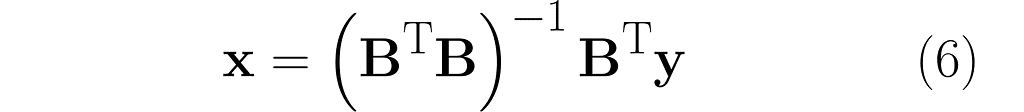
This is how it works in Python:
import numpy as np
# Tall matrix
B = [
[2, -3],
[1 , 0],
[3, -3]
]
# Convert to numpy array
B = np.array(B)
# A column vector from a lower-dimensional space
x = np.array([-3,1]).reshape(2,-1)
# Calculate its corresponding vector in a higher-dimensional space
y = B @ x
reconstructed_x = np.linalg.inv(B.T @ B) @ B.T @ y
print(reconstructed_x)
[[-3.] [ 1.]]
To summarize: the determinant measures the redundancy (or linear independence) of the columns and rows of a matrix. However, it only makes sense when applied to square matrices. Non-square matrices represent transformations between spaces of different dimensions and necessarily have linearly dependent columns or rows. If the target dimension is higher than the input dimension, it’s possible to reconstruct lower-dimensional vectors from higher-dimensional ones.
10. Inverse and Transpose: similarities and differences
You’ve certainly noticed that the inverse and transpose operations play a key role in matrix algebra. In this section, we bring together the most useful identities related to these operations.
Whenever I apply the inverse operator, I assume that the matrix being operated on is square.
We’ll start with the obvious one that hasn’t appeared yet.
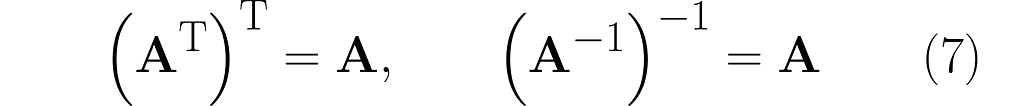
Here are the previously given identities (2) and (5), placed side by side:
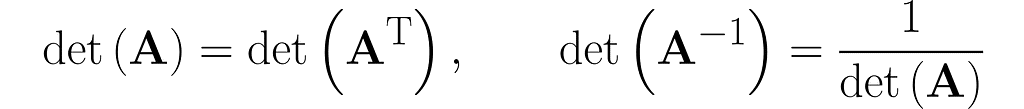
Let’s walk through the following reasoning, starting with the identity from equation (4), where A is replaced by the composite AB:
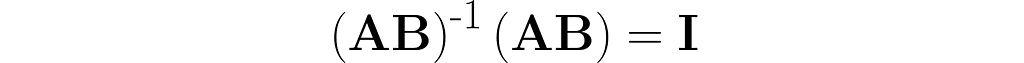
The parentheses on the right are not needed. After removing them, I right-multiply both sides by the matrix B⁻¹ and then by A⁻¹.
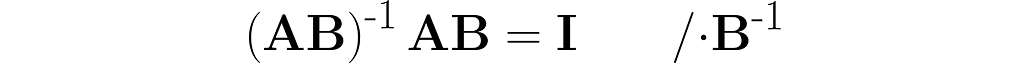
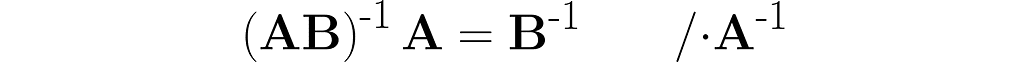
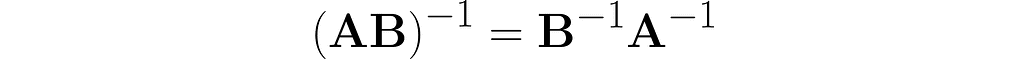
Thus, we observe the next similarity between inversion and transposition (see equation (3)):

You might be disappointed now, as the following only applies to transposition.
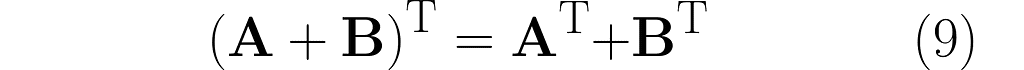
But imagine if A and B were scalars. The same for the inverse would be a mathematical scandal!
For a change, the identity in equation (4) works only for the inverse:
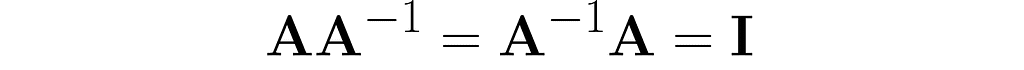
I’ll finish off this section by discussing the interplay between inversion and transposition.
From the last equation, along with equation (3), we get the following:
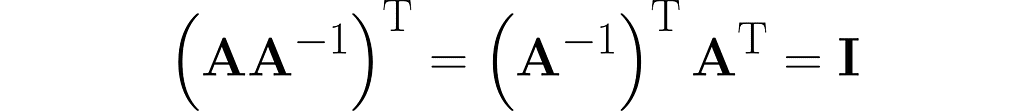
Keep in mind that Iᵀ = I. Right-multiplying by the inverse of Aᵀ yields the following identity:
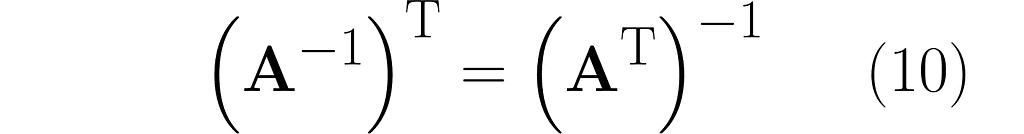
11. Translation by a vector
You might be wondering why I’m focusing only on the operation of multiplying a vector by a matrix, while neglecting the translation of a vector by adding another vector.
One reason is purely mathematical. Linear operations offer significant advantages, such as ease of transformation, simplicity of expressions, and algorithmic efficiency.
A key property of linear operations is that a linear combination of inputs leads to a linear combination of outputs:
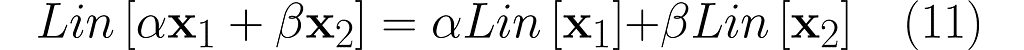
where α , β are real scalars, and Lin represents a linear operation.
Let’s first examine the matrix-vector multiplication operator Lin[x] = Ax from equation (1):
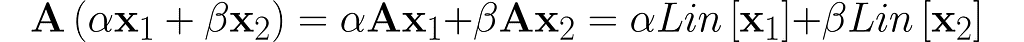
This confirms that matrix-vector multiplication is a linear operation.
Now, let’s consider a more general transformation, which involves a shift by a vector b:
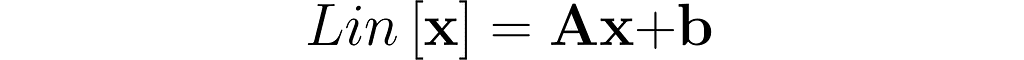
Plug in a weighted sum and see what comes out.
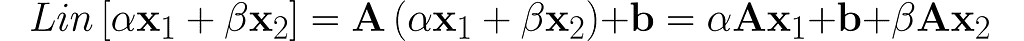
You can see that adding b disrupts the linearity. Operations like this are called affine to differentiate them from linear ones.
Don’t worry though — there’s a simple way to eliminate the need for translation. Simply shift the data beforehand, for example, by centering it, so that the vector b becomes zero. This is a common approach in data science.
Therefore, the data scientist only needs to worry about matrix-vector multiplication.
12. Final words
I hope that linear algebra seems easier to understand now, and that you’ve got a sense of how interesting it can be.
If I’ve sparked your interest in learning more, that’s great! But even if it’s just that you feel more confident with the course material, that’s still a win.
Bear in mind that this is more of a semi-formal introduction to the subject. For more rigorous definitions and proofs, you might need to look at specialised literature.
Unless otherwise noted, all images are by the author
References
[1] Gilbert Strang. Introduction to linear algebra. Wellesley-Cambridge Press, 2022.
[2] Marc Peter Deisenroth, A. Aldo Faisal, Cheng Soon Ong. Mathematics for machine learning. Cambridge University Press, 2020.
How to Interpret Matrix Expressions — Transformations was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.







